- Συγγραφέας Jason Gerald gerald@how-what-advice.com.
- Public 2024-02-01 14:12.
- Τελευταία τροποποίηση 2025-01-23 12:15.
Το μόνο που χρειάζεστε για να υπολογίσετε τη μέση ταχύτητα είναι η συνολική μετατόπιση. ή αλλαγή θέσης, και συνολικός χρόνος. Θυμηθείτε ότι η ταχύτητα υπολογίζει επίσης την κατεύθυνση και την ταχύτητα ενός αντικειμένου, οπότε συμπεριλάβετε μια κατεύθυνση στην απάντησή σας, όπως "βόρεια", "μπροστά" ή "αριστερά". Εάν το πρόβλημα υπολογισμού ταχύτητας περιλαμβάνει επίσης συνεχή επιτάχυνση, μπορείτε να μάθετε έναν γρήγορο τρόπο για να βρείτε την απάντηση ακόμη πιο εύκολα.
Βήμα
Μέθοδος 1 από 2: Υπολογισμός της μέσης ταχύτητας μετατόπισης και χρόνου

Βήμα 1. Να θυμάστε ότι η ταχύτητα περιλαμβάνει τόσο την ταχύτητα όσο και την κατεύθυνση ενός αντικειμένου
Η ταχύτητα περιγράφει τον ρυθμό με τον οποίο αλλάζει η θέση ενός αντικειμένου. Αυτό δεν έχει να κάνει μόνο με το πόσο γρήγορα κινείται το αντικείμενο, αλλά και με την κατεύθυνσή του. "100 μέτρα ανά δευτερόλεπτο νότια" είναι μια διαφορετική τιμή ταχύτητας από "100 μέτρα ανά δευτερόλεπτο ανατολικά".
- Οι ποσότητες που έχουν κατεύθυνση ονομάζονται διανυσματικά μεγέθη ». Αυτή η ποσότητα μπορεί να διακριθεί από μια ποσότητα χωρίς κατεύθυνση που ονομάζεται κλίμακα γράφοντας ένα βέλος πάνω από τη μεταβλητή. Για παράδειγμα, ο συμβολισμός v αντιπροσωπεύει τον ρυθμό, ενώ ο συμβολισμός v → αντιπροσωπεύει ταχύτητα ή ταχύτητα + κατεύθυνση. Ο συμβολισμός v που χρησιμοποιείται σε αυτό το άρθρο αντιπροσωπεύει την ταχύτητα.
- Σε επιστημονικά προβλήματα, θα πρέπει να χρησιμοποιείτε μετρητές ή άλλες μετρικές μονάδες για να εκφράσετε την απόσταση, ενώ για καθημερινούς σκοπούς μπορείτε να χρησιμοποιήσετε οποιαδήποτε μονάδα σας αρέσει.
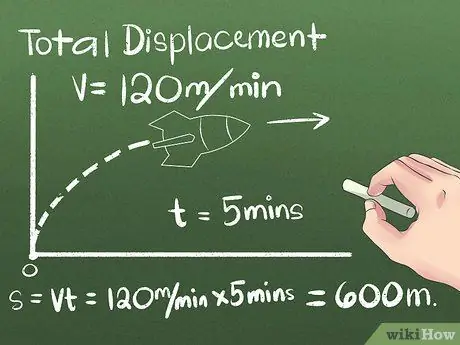
Βήμα 2. Βρείτε τη συνολική τιμή μετατόπισης
Μετατόπιση είναι η αλλαγή στη θέση ενός αντικειμένου, ή η απόσταση και η κατεύθυνση μεταξύ των σημείων εκκίνησης και λήξης του. Η κατεύθυνση που κινείται το αντικείμενο πριν φτάσει στην τελική του θέση μπορεί να αγνοηθεί, επειδή λαμβάνεται υπόψη μόνο η απόσταση μεταξύ των σημείων έναρξης και τέλους. Για το πρώτο παράδειγμα, θα χρησιμοποιήσουμε ένα αντικείμενο που κινείται με σταθερή ταχύτητα προς μία κατεύθυνση:
- Ας πούμε ότι ένας πύραυλος κινείται βόρεια για 5 λεπτά με σταθερή ταχύτητα 120 μέτρων το λεπτό. Για να υπολογίσετε την τελική θέση, χρησιμοποιήστε τον τύπο s = vt ή χρησιμοποιήστε πρακτική σκέψη για να υπολογίσετε την απόσταση που διανύει ο πύραυλος μετά από αυτό (5 λεπτά) (120 μέτρα/λεπτό) = 600 μέτρα βόρεια από το σημείο εκκίνησης.
- Για προβλήματα που συνεπάγονται συνεχή επιτάχυνση, μπορείτε να τα λύσετε με s = vt + at2, ή χρησιμοποιήστε τη σύντομη μέθοδο που περιγράφεται σε άλλη ενότητα για να βρείτε την απάντηση.
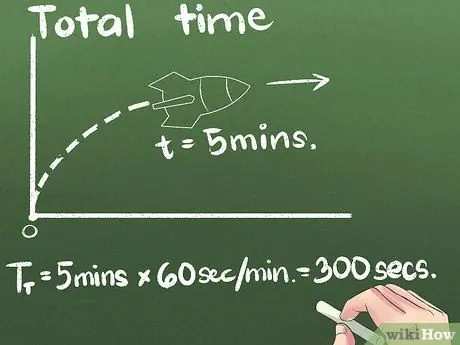
Βήμα 3. Βρείτε τον συνολικό χρόνο που αφιερώσατε
Στο παράδειγμά μας, ο πύραυλος προχωρά για 5 λεπτά. Μπορείτε να εκφράσετε τη μέση ταχύτητα σε οποιαδήποτε μονάδα χρόνου, αλλά η δεύτερη είναι η διεθνής επιστημονική τυπική μονάδα. Θα αλλάξουμε τις μονάδες δευτερολέπτων σε αυτό το παράδειγμα: (5 λεπτά) x (60 δευτερόλεπτα/λεπτό) = 300 δευτερόλεπτα.
Ακόμα και σε επιστημονικά προβλήματα, εάν η ερώτηση χρησιμοποιεί την ώρα ή μεγαλύτερη μονάδα χρόνου, θα είναι ευκολότερο να υπολογίσετε πρώτα την ταχύτητα και μετά να μετατρέψετε την τελική απάντηση σε μέτρα/δευτερόλεπτο
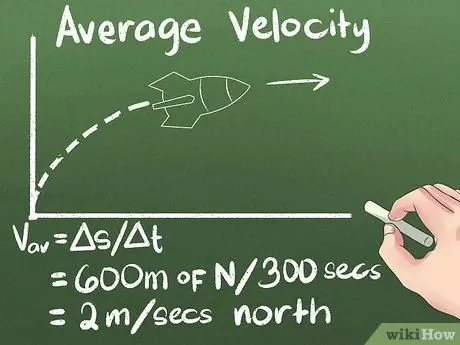
Βήμα 4. Υπολογίστε τη μέση ταχύτητα ως μετατόπιση με την πάροδο του χρόνου
Εάν γνωρίζετε πόσο μακριά κινείται ένα αντικείμενο και πόσο καιρό χρειάζεται για να φτάσετε εκεί, θα γνωρίζετε πόσο γρήγορα κινείται. Έτσι, για το παράδειγμα που χρησιμοποιούμε, η μέση ταχύτητα του πυραύλου είναι (600 μέτρα βόρεια) / (300 δευτερόλεπτα) = 2 μέτρα/δευτερόλεπτο βόρεια.
- Θυμηθείτε να συμπεριλάβετε μια κατεύθυνση (όπως "μπροστά" ή "βόρεια").
- Στον τύπο vav = s/Δt Το Το σύμβολο δέλτα σημαίνει "αλλαγή", οπότε s/Δt σημαίνει "αλλαγή θέσης σε μια χρονική περίοδο".
- Η μέση ταχύτητα μπορεί να γραφτεί ως vav, ή ως v με οριζόντια γραμμή από πάνω.

Βήμα 5. Λύστε πιο περίπλοκα προβλήματα
Εάν ένα αντικείμενο αλλάξει κατεύθυνση ή ταχύτητα, μην μπερδευτείτε. Η μέση ταχύτητα υπολογίζεται "μόνο" από τη συνολική μετατόπιση και τον συνολικό χρόνο. Τι συμβαίνει μεταξύ των σημείων έναρξης και λήξης μπορείτε να αγνοήσετε. Τα παρακάτω είναι μερικά παραδείγματα αντικειμένου που ταξιδεύει με την ίδια μετατόπιση και συνολικό χρόνο, και επομένως, την ίδια μέση ταχύτητα:
- Η Άννα περπατά δυτικά με 1 μέτρο/δευτερόλεπτο για 2 δευτερόλεπτα, μετά ξαφνικά επιταχύνει στα 3 μέτρα/δευτερόλεπτο και συνεχίζει το περπάτημα δυτικά για 2 δευτερόλεπτα. Η συνολική μετατόπιση είναι (1 m/s δυτικά) (2 sec) + (3 m/s δυτικά) (2 sec) = 8 μέτρα δυτικά. Ο συνολικός χρόνος είναι 2 δευτερόλεπτα + 2 δευτερόλεπτα = 4 δευτερόλεπτα. Άρα η μέση ταχύτητα είναι 8 μέτρα δυτικά/ 4 δευτερόλεπτα = 2 μέτρα/δεύτερο δυτικά.
-
Ο Μπαρτ περπατάει δυτικά με 5 μέτρα/δευτερόλεπτο για 3 δευτερόλεπτα, μετά γυρίζει και περπατά ανατολικά με 7 μέτρα/δευτερόλεπτο για 1 δευτερόλεπτο. Μπορούμε να σκεφτούμε την κίνηση προς τα ανατολικά ως "αρνητική κίνηση προς τα δυτικά", οπότε η συνολική μετατόπιση είναι = (5 μέτρα/δευτερόλεπτο προς τα δυτικά) (3 δευτερόλεπτα) + (-7 m/s δυτικά) (1 δευτερόλεπτο) = 8 μέτρα. Συνολικός χρόνος = 4 δευτερόλεπτα. Μέση ταχύτητα = 8 μέτρα δυτικά / 4 δευτερόλεπτα = 2 μέτρα/δεύτερο δυτικά.
-
Η Σάρλοτ περπάτησε βόρεια 1 μέτρο και μετά περπάτησε δυτικά 8 μέτρα, στη συνέχεια νότια 1 μέτρο. Ο χρόνος που απαιτείται για να ολοκληρωθεί ολόκληρο το ταξίδι είναι 4 δευτερόλεπτα. Σχεδιάστε το διάγραμμα σε ένα κομμάτι χαρτί και θα δείτε ότι το τελικό σημείο είναι 8 μέτρα δυτικά του σημείου εκκίνησης, οπότε αυτή η τιμή είναι η μετατόπιση. Ο συνολικός χρόνος που χρειάζεται είναι 4 δευτερόλεπτα, άρα η μέση ταχύτητα είναι 8 μέτρα δυτικά / 4 δευτερόλεπτα = 2 μέτρα/δεύτερο δυτικά.
Μέθοδος 2 από 2: Υπολογισμός της μέσης ταχύτητας της σταθερής επιτάχυνσης

Υπολογίστε τη μέση ταχύτητα Βήμα 6 Βήμα 1. Εξετάστε την αρχική ταχύτητα και τη σταθερή επιτάχυνση
Ας πούμε ότι το πρόβλημά μας είναι "Ένα ποδήλατο κινείται προς τα δεξιά με ταχύτητα 5 m/s, με σταθερή επιτάχυνση 2 m/s2Το Αν αυτό το ποδήλατο κινείται για 5 δευτερόλεπτα, ποια είναι η μέση ταχύτητά του;"
Εάν η μονάδα "μέτρο/δευτερόλεπτο2"για να σας μπερδέψουμε, γράψτε το ως" μέτρα/δευτερόλεπτο "ή" μέτρα ανά δευτερόλεπτο ανά δευτερόλεπτο ". Επιτάχυνση 2 μέτρων/δευτερόλεπτο/δευτερόλεπτο σημαίνει ότι η ταχύτητα αυξάνεται κατά 2 μέτρα ανά δευτερόλεπτο κάθε δευτερόλεπτο.

Υπολογίστε Μέση Ταχύτητα Βήμα 7 Βήμα 2. Χρησιμοποιήστε την επιτάχυνση για να βρείτε την τελική ταχύτητα
Η επιτάχυνση, που συμβολίζεται με το συμβολισμό α, είναι ο ρυθμός μεταβολής της ταχύτητας (ή του ρυθμού). Η ταχύτητα αυξάνεται με σταθερό ρυθμό αύξησης. Μπορείτε να σχεδιάσετε ένα τραπέζι χρησιμοποιώντας την επιτάχυνση για να βρείτε την ταχύτητα σε διαφορετικούς χρόνους καθ 'όλη τη διάρκεια του ποδηλάτου. Πρέπει να δημιουργήσουμε αυτόν τον πίνακα για να βρούμε το τελικό σημείο του προβλήματος (σε t = 5 δευτερόλεπτα), αλλά θα δημιουργήσουμε έναν μακρύτερο πίνακα για να σας διευκολύνουμε να κατανοήσετε αυτήν την έννοια:
- Στο σημείο εκκίνησης (χρόνος t = 0 δευτερόλεπτα), το ποδήλατο κινείται με ταχύτητα 5 μέτρων/δευτ.
- Μετά από 1 δευτερόλεπτο (t = 1), το ποδήλατο κινείται με ταχύτητα 5 μέτρων/δευτερόλεπτο + με = 5 μέτρα/δευτερόλεπτο + (2 μέτρα/δευτερόλεπτο2) (1 δευτερόλεπτο) = 7 μέτρα/δευτερόλεπτο.
- Στο t = 2, το ποδήλατο κινείται προς τα δεξιά με ταχύτητα 5+ (2) (2) = 9 μέτρα/δευτερόλεπτο.
- Στο t = 3, το ποδήλατο κινείται προς τα δεξιά με ταχύτητα 5+ (2) (3) = 11 μέτρα/δευτερόλεπτο.
- Στο t = 4, το ποδήλατο κινείται προς τα δεξιά με ταχύτητα 5+ (2) (4) = 13 μέτρα/δευτερόλεπτο.
- Στο t = 5, το ποδήλατο κινείται προς τα δεξιά με ταχύτητα 5+ (2) (5) = 15 μέτρα/δευτερόλεπτο.

Υπολογίστε Μέση Βήμα Βήμα 8 Βήμα 3. Χρησιμοποιήστε αυτόν τον τύπο για να βρείτε τη μέση ταχύτητα
Αν και "μόνο" εάν η επιτάχυνση είναι σταθερή, η μέση ταχύτητα θα είναι ίση με τη μέση τιμή του αθροίσματος της τελικής και της αρχικής ταχύτητας. (vφά +vΕγώ)/2 Το Για το παραπάνω πρόβλημά μας, η αρχική ταχύτητα του ποδηλάτου είναι vΕγώ 5 μέτρα/δευτερόλεπτο. Αφού υπολογίσουμε, η τελική ταχύτητα είναι vφά 15 μέτρα/δευτερόλεπτο. Προσθέτοντας αυτές τις δύο τιμές μαζί, παίρνουμε (15 μέτρα/δευτερόλεπτο + 5 μέτρα/δευτερόλεπτο)/2 = (20 μέτρα/δευτερόλεπτο)/2 = 10 μέτρα/δευτερόλεπτο δεξιά κατεύθυνση.
- Θυμηθείτε να συμπεριλάβετε την κατεύθυνση, σε αυτήν την περίπτωση "δεξιά".
- Αυτός ο όρος μπορεί να γραφτεί ως v0 (ταχύτητα στο χρόνο 0, ή αρχική ταχύτητα) και v (τελική ταχύτητα).

Υπολογίστε Μέσο Βήμα Βήμα 9 Βήμα 4. Κατανοήστε διαισθητικά τον τύπο μέσης ταχύτητας
Για να βρούμε τη μέση ταχύτητα, μπορούμε να χρησιμοποιήσουμε την ταχύτητα σε οποιοδήποτε σημείο και να βρούμε τον μέσο όρο για όλα αυτά. (Αυτός είναι ο ορισμός του μέσου όρου.) Επειδή αυτό απαιτεί λογισμό ή άπειρο χρόνο, κατανοήστε αυτόν τον τύπο πιο διαισθητικά. Αντί να παίρνετε κάθε φορά, υπολογίστε τη μέση ταχύτητα των δύο χρονικών σημείων και δείτε τα αποτελέσματα. Ένα χρονικό σημείο είναι κοντά στην αρχή της βόλτας, όπου η μοτοσυκλέτα πηγαίνει αργά και ένα άλλο σημείο είναι κοντά στο τελικό σημείο όπου η μοτοσυκλέτα πηγαίνει γρήγορα.

Υπολογίστε Μέσο Βήμα Βήμα 10 Βήμα 5. Δοκιμάστε τη διαισθητική θεωρία
Χρησιμοποιήστε τον παραπάνω πίνακα για να προσδιορίσετε την ταχύτητα σε διαφορετικά χρονικά σημεία. Ορισμένα ζεύγη που πληρούν τα κριτήριά μας είναι (t = 0, t = 5), (t = 1, t = 4) ή (t = 2, t = 3). Μπορείτε να δοκιμάσετε αυτόν τον τύπο με τιμές t εκτός από ακέραιους αριθμούς, αν θέλετε.
Όποιο ζεύγος σημείων και αν επιλέξετε, η μέση ταχύτητα εκείνη τη στιγμή θα είναι πάντα η ίδια. Για παράδειγμα, ((5+15)/2), ((7+13)/2) ή ((9+11)/2) όλα ίσα 10 μέτρα/δευτερόλεπτο προς τα δεξιά

Υπολογίστε Μέση Ταχύτητα Βήμα 11 Βήμα 6. Συμπληρώστε τη διαισθητική εξήγηση
Εάν χρησιμοποιήσουμε αυτήν τη μέθοδο με μια λίστα με κάθε φορά που λαμβάνεται, θα συνεχίσουμε να υπολογίζουμε τον μέσο όρο του πρώτου μισού του ταξιδιού και του δεύτερου μισού του ταξιδιού. Ο χρόνος που απαιτείται για την κάλυψη κάθε ημιχρόνου είναι ο ίδιος, οπότε δεν χάνεται ταχύτητα όταν ολοκληρώσουμε την καταμέτρηση.
- Δεδομένου ότι οποιοδήποτε ζεύγος θα δώσει το ίδιο αποτέλεσμα, ο μέσος όρος αυτών των ταχυτήτων θα είναι επίσης ο ίδιος σε αξία. Στο παράδειγμά μας, η ταχύτητα του συνόλου είναι "10 μέτρα/δευτερόλεπτο προς τα δεξιά" θα εξακολουθεί να είναι 10 μέτρα/δευτερόλεπτο προς τα δεξιά.
- Μπορούμε να βρούμε αυτήν την τιμή υπολογίζοντας τον μέσο όρο οποιουδήποτε ζεύγους, για παράδειγμα την αρχική και την τελική ταχύτητα. Στο παράδειγμά μας, αυτές οι ταχύτητες επιτυγχάνονται σε t = 0 και t = 5 και μπορούν να υπολογιστούν χρησιμοποιώντας τον παραπάνω τύπο: (5+15)/2 = 10 μέτρα/δευτερόλεπτο στα δεξιά.

Υπολογίστε Μέσο Βήμα Βήμα 12 Βήμα 7. Κατανοήστε μαθηματικά αυτόν τον τύπο
Εάν είστε πιο άνετοι με τις αποδείξεις που γράφονται ως τύποι, μπορείτε να ξεκινήσετε με έναν τύπο για να υπολογίσετε την απόσταση που διανύθηκε υποθέτοντας σταθερή επιτάχυνση και να αντλήσετε τον τύπο από εκεί:
- s = vΕγώt + στο2Το (Τεχνικά s και t, ή αλλαγή θέσης και αλλαγή χρόνου, αλλά θα καταλαβαίνατε επίσης αν γράφατε s και t.)
- Μέση ταχύτητα vav ορίζεται ως s/t, οπότε εισαγάγετε τον τύπο στη μορφή s/t
- vav = s/t = vΕγώ + στο
- Ο χρόνος επιτάχυνσης x είναι ίσος με τη μεταβολή της συνολικής ταχύτητας, ή vφά - vΕγώΤο Μπορούμε λοιπόν να αντικαταστήσουμε το "at" στον τύπο και να πάρουμε:
- vav = vΕγώ + (vφά - vΕγώ).
- Απλοποιήστε: vav = vΕγώ + vφά - vΕγώ = vΕγώ + vφά = (vφά +vΕγώ)/2.
Συμβουλές
- Η ταχύτητα διαφέρει από την ταχύτητα επειδή η ταχύτητα είναι ένα διανυσματικό μέγεθος ενώ η ταχύτητα είναι ένα κλιμακωτό μέγεθος. Τα διανυσματικά μεγέθη περιλαμβάνουν τόσο την κατεύθυνση όσο και το μέγεθος, ενώ τα κλιμακωτά μεγέθη περιλαμβάνουν μόνο το μέγεθος.
- Εάν το αντικείμενο κινείται σε μία διάσταση, όπως αριστερά-δεξιά, μπορείτε να χρησιμοποιήσετε έναν θετικό αριθμό για να αναπαραστήσετε μια κατεύθυνση (όπως δεξιά) και έναν αρνητικό αριθμό για να αναπαραστήσετε μια άλλη κατεύθυνση (αριστερά). Γράψτε αυτόν τον συμβολισμό στο επάνω μέρος της σελίδας σας, έτσι ώστε να είναι σαφής σε άτομα που διαβάζουν τη δουλειά σας.






