- Συγγραφέας Jason Gerald [email protected].
- Public 2023-12-16 11:05.
- Τελευταία τροποποίηση 2025-01-23 12:15.
Η τετραγωνική ρίζα ενός αριθμού είναι εύκολο να βρεθεί εάν η απάντηση είναι ένας ακέραιος αριθμός. Εάν η απάντηση δεν είναι ακέραιος, υπάρχει μια σειρά διαδικασιών που μπορείτε να ακολουθήσετε για να λάβετε την τετραγωνική ρίζα, ακόμη και αν δεν χρησιμοποιείτε αριθμομηχανή. Για αυτό πρέπει να κατανοήσετε τα βασικά του πολλαπλασιασμού, της προσθήκης και της διαίρεσης.
Βήμα
Μέθοδος 1 από 3: Εύρεση της τετραγωνικής ρίζας ενός ακέραιου
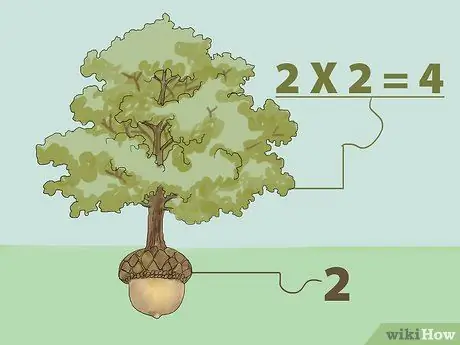
Βήμα 1. Βρείτε την τέλεια τετραγωνική ρίζα πολλαπλασιάζοντας
Η τετραγωνική ρίζα ενός αριθμού είναι ένας αριθμός που όταν πολλαπλασιαστεί με τον εαυτό του επιστρέφει τον αρχικό αριθμό. Με άλλα λόγια: "Τι αριθμό μπορούμε να πολλαπλασιάσουμε από μόνο του για να πάρουμε τον αριθμό που θέλουμε;"
- Για παράδειγμα, η τετραγωνική ρίζα του 1 είναι 1 επειδή το 1 πολλαπλασιασμένο με 1 είναι 1 (1Χ1 = 1). Έτσι, η τετραγωνική ρίζα του 4 είναι 2 επειδή το 2 πολλαπλασιασμένο με το 2 είναι 4 (2X2 = 4). Σκεφτείτε την έννοια της τετραγωνικής ρίζας ως δέντρο. Ένα δέντρο μεγαλώνει από σπόρους. Έτσι, ένα δέντρο είναι μεγαλύτερο από έναν σπόρο, ο οποίος αναπτύσσεται από έναν σπόρο που είναι η ρίζα του. Από το παραπάνω παράδειγμα, 4 είναι το δέντρο και 2 είναι ο σπόρος.
- Έτσι, η τετραγωνική ρίζα του 9 είναι 3 (3X3 = 9), του 16 είναι 4 (4X4 = 16), του 25 είναι 5 (5X5 = 25), του 36 είναι 6 (6X6 = 36), του 49 είναι 7 (7X7 = 49), από 64 είναι 8 (8X8 = 64), από 81 είναι 9 (9X9 = 81) και από 100 είναι 10 (10X10 = 100).
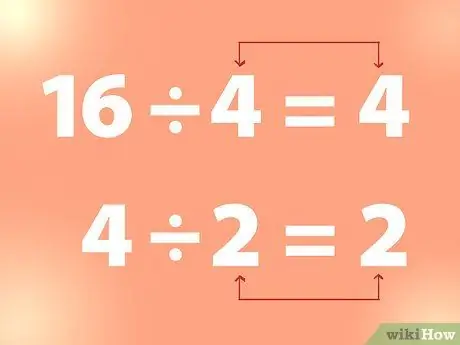
Βήμα 2. Χρησιμοποιήστε συνεχή διαίρεση για να βρείτε την τετραγωνική ρίζα
Για να βρείτε την τετραγωνική ρίζα ενός ακέραιου, μπορείτε να διαιρέσετε τον ακέραιο με έναν αριθμό έως ότου λάβετε έναν αριθμό που ισούται με τον διαιρέτη.
- Παράδειγμα: 16 διαιρούμενο με 4 είναι 4. Και το 4 διαιρούμενο με 2 είναι 2, και ούτω καθεξής. Έτσι, από το παραπάνω παράδειγμα, το 4 είναι η τετραγωνική ρίζα του 16 και το 2 είναι η τετραγωνική ρίζα του 4.
- Οι τέλειες τετραγωνικές ρίζες δεν έχουν κλάσματα ή δεκαδικά επειδή είναι ακέραιοι αριθμοί.
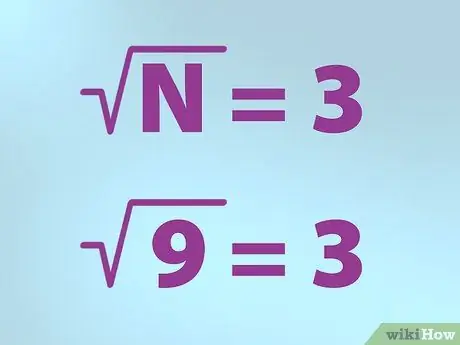
Βήμα 3. Χρησιμοποιήστε το σωστό σύμβολο για την τετραγωνική ρίζα
Οι μαθηματικοί χρησιμοποιούν ένα ειδικό σύμβολο για να αναπαραστήσουν την τετραγωνική ρίζα. Το σχήμα είναι σαν ένα σημάδι επιλογής με μια γραμμή πάνω δεξιά.
- Το N ισούται με τον αριθμό για τον οποίο θέλετε να βρείτε την τετραγωνική ρίζα. Το Ν τοποθετείται κάτω από το σημάδι ελέγχου.
- Έτσι, εάν θέλετε να βρείτε την τετραγωνική ρίζα του 9, γράψτε έναν τύπο βάζοντας το "Ν" (9) μέσα σε ένα σημάδι ελέγχου (σύμβολο "ρίζα"), στη συνέχεια γράψτε ένα σύμβολο ίσου και ακολουθούμενο από το 3. σημαίνει "τετραγωνική ρίζα του Το 9 είναι ίσο με 3 ".
Μέθοδος 2 από 3: Εύρεση της τετραγωνικής ρίζας ενός άλλου αριθμού
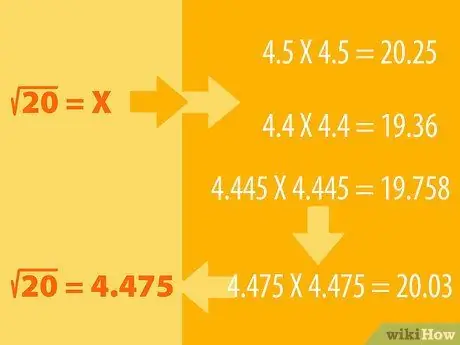
Βήμα 1. Μαντέψτε και κάντε τη διαδικασία της εξάλειψης
Είναι δύσκολο να βρεθεί η τετραγωνική ρίζα ενός μη ακέραιου αριθμού. Ωστόσο, αυτό δεν σημαίνει ότι είναι αδύνατο.
- Για παράδειγμα, ας πούμε ότι θέλετε να βρείτε την τετραγωνική ρίζα του 20. Γνωρίζουμε ότι το 16 είναι ένα τέλειο τετράγωνο του οποίου η τετραγωνική ρίζα είναι 4 (4X4 = 16). Τότε οι 25 τετραγωνικές ρίζες είναι 5 (5Χ5 = 25), άρα η τετραγωνική ρίζα του 20 πρέπει να βρίσκεται μεταξύ των δύο.
- Μπορείτε να μαντέψετε ότι η τετραγωνική ρίζα του 20 είναι 4.5. Τώρα τετράγωνο 4.5 για να δείτε το αποτέλεσμα. Δηλαδή, πολλαπλασιάζουμε το 4, 5 από μόνο του: 4, 5Χ4, 5. Δείτε αν η απάντηση είναι μεγαλύτερη ή μικρότερη από 20. Εάν η εικασία σας είναι πολύ μακριά, δοκιμάστε έναν άλλο αριθμό (π.χ. 4, 6 ή 4, 4) και προσαρμόστε μαντέψτε αναλόγως. εσείς μέχρι να πάρετε τον αριθμό 20.
- Για παράδειγμα, 4, 5X4, 5 = 20, 25, οπότε λογικά πρέπει να βρούμε έναν μικρότερο αριθμό, ίσως 4, 4. 4, 4X4, 4 = 19, 36. Άρα, η τετραγωνική ρίζα του 20 πρέπει να βρίσκεται μεταξύ 4, 5 και 4, 4. Δοκιμάστε με 4, 445X4, 445. Το αποτέλεσμα είναι 19, 758. Το αποτέλεσμα πλησιάζει. Συνεχίστε να προσπαθείτε με άλλους αριθμούς μέχρι να λάβετε 4, 475X4, 475 = 20, 03. Στρογγυλοποιημένος, αυτός ο αριθμός ισούται με 20.

Βήμα 2. Χρησιμοποιήστε τη διαδικασία μέσου όρου
Αυτή η διαδικασία ξεκινά επίσης με την εύρεση των δύο πλησιέστερων τέλειων τετραγώνων που πλαισιώνονται από τον αριθμό.
- Στη συνέχεια, διαιρέστε αυτόν τον αριθμό με μία από τις τέλειες τετραγωνικές ρίζες. Λάβετε την απάντηση και, στη συνέχεια, βρείτε τον μέσο όρο μεταξύ αυτού του αριθμού και του αριθμού που θέλετε να βρείτε τη ρίζα (μπορείτε να βρείτε τον μέσο όρο προσθέτοντας τα δύο μαζί και διαιρώντας με δύο). Στη συνέχεια διαιρέστε τον αρχικό αριθμό με τον μέσο όρο που λαμβάνεται. Το τελευταίο βήμα, βρείτε τον μέσο όρο των αποτελεσμάτων με τον μέσο όρο που υπολογίστηκε την πρώτη φορά.
- Ακούγεται περίπλοκο; Θα ήταν ευκολότερο να δοθεί ένα παράδειγμα. Για παράδειγμα, 10 βρίσκεται ανάμεσα στα δύο τέλεια τετράγωνα 9 (3X3 = 9) και 16 (4X4 = 16). Οι τετραγωνικές ρίζες και των δύο αριθμών είναι 3 και 4. Άρα, διαιρέστε το 10 με τον πρώτο αριθμό, 3. Το αποτέλεσμα είναι 3, 33. Τώρα βρείτε τον μέσο όρο των 3 και 3, 33 προσθέτοντάς τους μαζί και διαιρώντας με το 2. Το αποτέλεσμα είναι 3, 1667 Τώρα διαιρέστε το 10 με το 3.1667. Το αποτέλεσμα είναι 3.1579. Στη συνέχεια βρείτε το μέσο όρο των 3.1579 και 3.1667 προσθέτοντάς τα και διαιρώντας με το 2. Το αποτέλεσμα είναι 3.1623.
- Ελέγξτε το αποτέλεσμα πολλαπλασιάζοντας την απάντηση (σε αυτό το παράδειγμα 3, 1623) από μόνη της. Το αποτέλεσμα του 3.1623 πολλαπλασιασμένο με 3.1623 αποδεικνύεται ότι είναι 10.001.
Μέθοδος 3 από 3: Τετραγωνισμός αρνητικών αριθμών
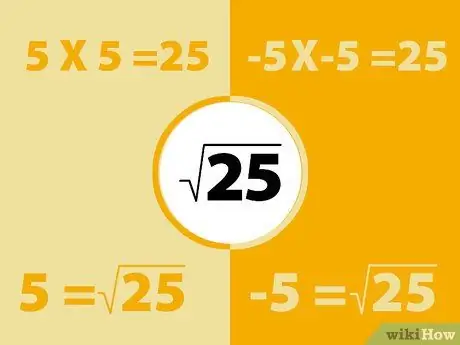
Βήμα 1. Τετραγωνίστε αρνητικούς αριθμούς χρησιμοποιώντας την ίδια μέθοδο
Θυμηθείτε ότι οι αρνητικοί χρόνοι αρνητικοί είναι θετικοί. Έτσι, το τετράγωνο ενός αρνητικού αριθμού θα παράγει έναν θετικό αριθμό.
- Για παράδειγμα, -5X -5 = 25. Ωστόσο, θυμηθείτε επίσης ότι 5x5 = 25. Έτσι η τετραγωνική ρίζα του 25 μπορεί να είναι -5 ή 5. Βασικά κάθε αριθμός έχει δύο τετραγωνικές ρίζες.
- Ομοίως, 3X3 = 9 και -3X -3 = 9, οπότε οι τετραγωνικές ρίζες του 9 είναι 3 και -3. Η θετική τετραγωνική ρίζα ονομάζεται "κύρια ρίζα". Σε αυτό το σημείο, πρέπει απλώς να δώσουμε προσοχή σε αυτήν την απάντηση.
Βήμα 2. Χρησιμοποιήστε μια αριθμομηχανή
Παρόλο που είναι καλύτερο να μπορείτε να κάνετε τα μαθηματικά με το χέρι, υπάρχουν πολλές διαθέσιμες ηλεκτρονικές αριθμομηχανές για τον υπολογισμό των τετραγωνικών ριζών.
- Αναζητήστε το κουμπί τετραγωνικής ρίζας σε μια κανονική αριθμομηχανή.
- Στην ηλεκτρονική αριθμομηχανή, εισαγάγετε απευθείας τον αριθμό για τον οποίο θέλετε να βρείτε την τιμή της τετραγωνικής ρίζας και κάντε κλικ στο κουμπί. Ο υπολογιστής θα σας δείξει την τιμή της τετραγωνικής ρίζας.
Συμβουλές
-
Έχετε πάντα υπόψη μερικά σημαντικά τέλεια τετράγωνα:
- 02 = 0, 12 = 1, 32 = 9, 42 = 16, 52 = 25, 62 = 36, 72 = 49, 82 = 64, 92 = 81, 102 = 100,
- Θυμηθείτε επίσης αυτό το τέλειο τετράγωνο: 112 = 121, 122 = 144, 132 169, 142 = 196, 152 = 225, 162 = 256, 172 = 289…
- Σημειώστε επίσης αυτό: 102 = 100, 202 = 400, 302 = 900, 402 = 1600, 502 = 2500, …






