- Συγγραφέας Jason Gerald [email protected].
- Public 2024-02-01 14:12.
- Τελευταία τροποποίηση 2025-01-23 12:15.
Η μετατόπιση στη φυσική υποδηλώνει μια αλλαγή στη θέση ενός αντικειμένου. Όταν υπολογίζετε τη μετατόπιση, υπολογίζετε πόσο μακριά βρίσκεται ένα αντικείμενο με βάση τις αρχικές και τελικές θέσεις του. Ο τύπος που χρησιμοποιείτε για τον υπολογισμό της μετατόπισης εξαρτάται από τη μεταβλητή που δίνεται στο πρόβλημα. Ακολουθήστε αυτά τα βήματα για να υπολογίσετε τη μετατόπιση.
Βήμα
Μέρος 1 από 5: Υπολογισμός της προκύπτουσας μετατόπισης

Βήμα 1. Χρησιμοποιήστε τον τύπο μετατόπισης που προκύπτει εάν η μονάδα απόστασης χρησιμοποιείται για να υποδείξει τις θέσεις έναρξης και λήξης
Αν και η απόσταση είναι διαφορετική από τη μετατόπιση, το πρόβλημα μετατόπισης που προκύπτει αναζητά πόσα χιλιόμετρα ή μέτρα έχει διανύσει το αντικείμενο. Θα χρησιμοποιήσετε αυτήν τη μονάδα μέτρησης για να υπολογίσετε τη μετατόπιση και πόσο μακριά η τοποθεσία ενός αντικειμένου αποκλίνει από το σημείο εκκίνησης.
- Ο τύπος μετατόπισης που προκύπτει γράφεται ως εξής: S = x²+y² Το S είναι η μετατόπιση. Το Χ είναι η πρώτη φορά κίνησης του αντικειμένου και το Υ είναι η δεύτερη φορά κίνησης του αντικειμένου. Εάν το αντικείμενό σας κινείται μόνο προς μία κατεύθυνση, τότε Y = 0.
- Ένα αντικείμενο μπορεί να κινηθεί μόνο κατά μέγιστο δύο κατευθύνσεις επειδή η κίνηση κατά μήκος άξονα βορρά/νότου ή ανατολής/δύσης θεωρείται ουδέτερη κίνηση.

Βήμα 2. Συνδέστε τις κουκκίδες κατά σειρά κίνησης και επισημάνετε τις από το Α-Ζ
Χρησιμοποιήστε έναν χάρακα για να σχεδιάσετε μια ευθεία γραμμή από σημείο σε σημείο.
- Επίσης, θυμηθείτε να συνδέσετε το σημείο εκκίνησης με το τελικό σημείο χρησιμοποιώντας μια ευθεία γραμμή. Αυτή είναι η μετατόπιση που θα υπολογίσουμε.
- Για παράδειγμα, εάν ένα αντικείμενο κινείται ανατολικά 300 m και βόρεια 400 m, θα σχηματίσει ορθογώνιο τρίγωνο. Το AB θα είναι το πρώτο σκέλος του τριγώνου και το BC θα είναι το δεύτερο σκέλος. Το AC θα είναι η υποτείνουσα του τριγώνου και το μέγεθος του είναι η μετατόπιση του αντικειμένου. Σε αυτό το παράδειγμα, οι δύο κατευθύνσεις είναι ανατολική και βόρεια.

Βήμα 3. Εισαγάγετε τιμές για x² και y²
Τώρα που γνωρίζετε τις δύο κατευθύνσεις κίνησης του αντικειμένου σας, εισαγάγετε τις τιμές στις κατάλληλες μεταβλητές.
Για παράδειγμα, x = 300 και y = 400. Ο τύπος σας πρέπει να μοιάζει με αυτόν: S = 300² + 400²
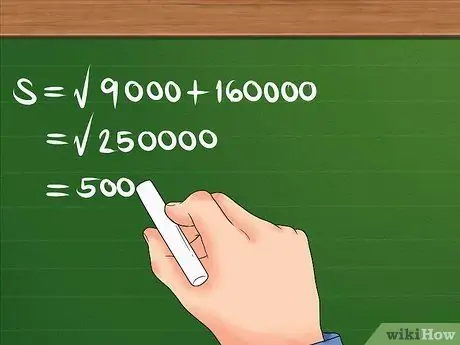
Βήμα 4. Υπολογίστε τον τύπο χρησιμοποιώντας τη σειρά των πράξεων
Πρώτα τα τετράγωνα 300 και 400, στη συνέχεια προσθέστε τα και βρείτε την τετραγωνική ρίζα του αθροίσματος.
Για παράδειγμα: S = 90000 + 160000. S = 250000. S = 500. Τώρα ξέρετε ότι η μετατόπιση είναι 500 m
Μέρος 2 από 5: Όταν η ταχύτητα και ο χρόνος είναι γνωστοί

Βήμα 1. Χρησιμοποιήστε αυτόν τον τύπο όταν το πρόβλημα σας λέει την ταχύτητα ενός αντικειμένου και το χρόνο που χρειάζεται
Ορισμένα μαθηματικά προβλήματα δεν θα σας πουν πόσο μακριά ή πόσο γρήγορα κινείται ένα αντικείμενο. Μπορείτε να υπολογίσετε την μετατόπιση χρησιμοποιώντας αυτό το μέγεθος χρόνου και ταχύτητας.
-
Σε αυτήν την περίπτωση, ο τύπος γίνεται: S = 1/2 (u + v) t
U = αρχική ταχύτητα του αντικειμένου ή πόσο γρήγορα το αντικείμενο αρχίζει να κινείται προς μια συγκεκριμένη κατεύθυνση. V = η τελική ταχύτητα του αντικειμένου ή το πόσο γρήγορα το αντικείμενο κινείται προς την τελική του θέση. T = ο χρόνος που χρειάζεται το αντικείμενο για να φτάσει στην τελική του θέση.
- Παράδειγμα: Ένα αυτοκίνητο κατεβαίνει στο δρόμο για 45 δευτερόλεπτα (απαιτείται χρόνος). Το αυτοκίνητο στρίβει δυτικά με 20 m/s (αρχική ταχύτητα) και στο τέλος του δρόμου, η ταχύτητά του είναι 23 m/s (τελική ταχύτητα). Υπολογίστε τη μετατόπιση με βάση αυτούς τους παράγοντες.

Βήμα 2. Εισαγάγετε την απαιτούμενη ταχύτητα και χρόνο στις κατάλληλες μεταβλητές
Τώρα που γνωρίζετε πόσο μακριά κινείται το αυτοκίνητο, πόσο γρήγορα κινείται το αυτοκίνητο στην αρχή και στο τέλος, μπορείτε να βρείτε την απόσταση από την τοποθεσία εκκίνησης έως την τελική τοποθεσία.
Ο τύπος σας πρέπει να μοιάζει με αυτόν: S = 1/2 (20 + 23) 45

Βήμα 3. Υπολογίστε τον τύπο αφού τοποθετήσετε τις τιμές στη σωστή θέση
Θυμηθείτε να ακολουθήσετε τη σειρά των λειτουργιών, διαφορετικά οι μετατοπίσεις θα έχουν ως αποτέλεσμα πολύ διαφορετικές τιμές.
- Για αυτόν τον τύπο, δεν έχει σημασία αν κατά λάθος αλλάξετε τις ταχύτητες έναρξης και λήξης. Δεδομένου ότι θα προσθέσετε πρώτα αυτούς τους αριθμούς μαζί, δεν έχει σημασία πού βρίσκονται σε παρένθεση. Ωστόσο, για άλλους τύπους, η εναλλαγή της αρχικής και της τελικής ταχύτητας θα έχει ως αποτέλεσμα διαφορετικές τιμές μετατόπισης.
- Ο τύπος σας πρέπει να μοιάζει με αυτόν: S = 1/2 (43) 45. Πρώτα διαιρέστε 43 με 2, το οποίο έχει ως αποτέλεσμα 21, 5. Στη συνέχεια πολλαπλασιάστε το 21, το 5 με το 45, οπότε το αποτέλεσμα είναι 967,5 μέτρα. 967, 5 είναι το μέγεθος του κυβισμού σας ή πόσο μακριά έχει μετακινηθεί το αυτοκίνητό σας από την αφετηρία του.
Μέρος 3 από 5: Όταν είναι γνωστή η αρχική ταχύτητα, επιτάχυνση και χρόνος
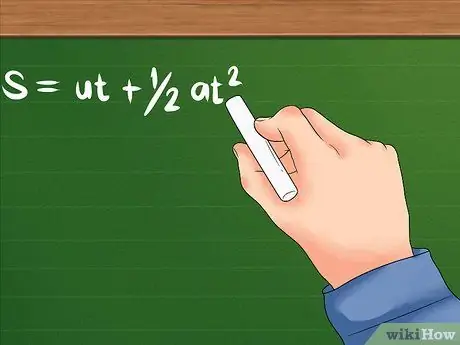
Βήμα 1. Χρησιμοποιήστε τον τροποποιημένο τύπο όταν η επιτάχυνση είναι γνωστή επιπλέον της αρχικής ταχύτητας και χρόνου
Ορισμένες ερωτήσεις θα σας πουν μόνο πόσο γρήγορα κινείται το αντικείμενο στην αρχή, πόσο γρήγορα το αντικείμενο αρχίζει να επιταχύνεται και πόσο μακριά κινείται το αντικείμενο. Θα χρειαστείτε τον παρακάτω τύπο.
- Ο τύπος για αυτό το πρόβλημα είναι: S = ut + 1/2at² Το Το U εξακολουθεί να δείχνει την αρχική ταχύτητα. α είναι η επιτάχυνση του αντικειμένου ή πόσο γρήγορα αρχίζει να αλλάζει η ταχύτητά του. Το T μπορεί να σημαίνει το χρόνο που χρειάζεται ή ένα ορισμένο χρονικό διάστημα που χρειάζεται ένα αντικείμενο για να επιταχυνθεί. Και οι δύο θα χρησιμοποιήσουν μονάδες χρόνου όπως δευτερόλεπτα, ώρες και άλλες.
- Ας υποθέσουμε ότι ένα αυτοκίνητο που κινείται με 25 m/s (αρχική ταχύτητα) αρχίζει να επιταχύνει με 3 m/s2 (επιτάχυνση) για 4 δευτερόλεπτα (χρόνος). Ποιος είναι ο κυβισμός του αυτοκινήτου μετά από 4 δευτερόλεπτα;

Βήμα 2. Εισαγάγετε τις τιμές στον τύπο
Σε αντίθεση με τον προηγούμενο τύπο, εδώ εμφανίζεται μόνο η αρχική ταχύτητα, οπότε βεβαιωθείτε ότι έχετε εισαγάγει τα σωστά δεδομένα.
Με βάση τα παραπάνω δείγματα δεδομένων, ο τύπος σας θα μοιάζει με αυτόν: S = 25 (4) + 1/2 (3) 4². Βοηθά στην προσθήκη παρενθέσεων γύρω από το μέγεθος και το χρόνο επιτάχυνσης για να σας βοηθήσει να διαχωρίσετε τους αριθμούς
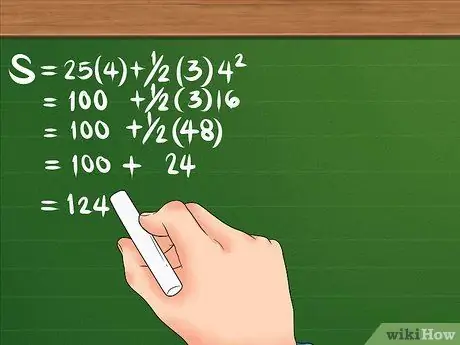
Βήμα 3. Υπολογίστε τη μετατόπιση κάνοντας τη με τη σωστή σειρά λειτουργιών
Ένας γρήγορος τρόπος για να σας βοηθήσει να θυμηθείτε την ακολουθία των πράξεων είναι η γαϊδουρογέφυρα Kur ir Kua ci Kadang Ba wa Juragan Turtles. Αυτό αντιπροσωπεύει τη σωστή σειρά: παρενθέσεις, τετράγωνα, πολλαπλασιασμός, διαίρεση, πρόσθεση και αφαίρεση.
Ας δούμε ξανά τον τύπο: S = 25 (4) + 1/2 (3) 4². Πρώτα, τετράγωνο 4, το αποτέλεσμα είναι 16. Στη συνέχεια, πολλαπλασιάστε το 16 επί 3, κάνοντας 48. τότε πολλαπλασιάστε επίσης το 25 επί 4, για να κάνετε το 100. Διαιρέστε το 48 με το 2, για να κάνετε το 24. Η εξίσωση σας πρέπει να μοιάζει με αυτήν: S = 100 + 24. Μόλις προσθέσετε τα δύο μαζί, η μετατόπιση είναι 124 μέτρα
Μέρος 4 από 5: Υπολογισμός της γωνιακής μετατόπισης

Βήμα 1. Βρείτε τη γωνιακή μετατόπιση καθώς το αντικείμενο κινείται σε μια κυκλική διαδρομή
Παρόλο που εξακολουθείτε να υπολογίζετε τη μετατόπιση χρησιμοποιώντας μια ευθεία γραμμή, θα πρέπει να βρείτε τη διαφορά μεταξύ των θέσεων έναρξης και λήξης του αντικειμένου καθώς κινείται σε μια κυκλική διαδρομή.
- Φανταστείτε ένα κορίτσι να κάθεται σε ένα γύρο. Καθώς περιστρέφεται με το γαϊτανάκι, θα κινηθεί σε κυκλικό μονοπάτι. Η γωνιακή μετατόπιση προσπαθεί να βρει τη μικρότερη απόσταση μεταξύ της αρχικής και της τελικής θέσης όταν το αντικείμενο δεν κινείται σε ευθεία γραμμή.
- Ο τύπος για τη γωνιακή μετατόπιση είναι: = S/r, όπου S είναι η γραμμική μετατόπιση, r είναι η ακτίνα και είναι η γωνιακή μετατόπιση. Η γραμμική μετατόπιση είναι το πόσο μακριά ένα αντικείμενο κινείται κατά μήκος ενός τόξου. Η ακτίνα είναι η απόσταση του αντικειμένου από το κέντρο του κύκλου. Η γωνιακή μετατόπιση είναι η τιμή που θέλουμε να βρούμε.

Βήμα 2. Συνδέστε τη γραμμική μετατόπιση και την ακτίνα στην εξίσωση
Θυμηθείτε ότι η ακτίνα είναι η απόσταση από το κέντρο του κύκλου. κάποια προβλήματα θα σας πουν τη διάμετρο ενός κύκλου, η οποία πρέπει να διαιρεθεί με 2 για να βρεθεί η ακτίνα.
- Ακολουθεί ένα παράδειγμα προβλήματος: Ένα κορίτσι κάνει βόλτα με τα πόδια. Το κάθισμα απέχει 1 μέτρο από το κέντρο του κύκλου (η ακτίνα). Εάν το κορίτσι κινείται σε τροχιά τόξου 1,5 μέτρα (γραμμική μετατόπιση), ποια είναι η γωνιακή της μετατόπιση;
- Η εξίσωση σας θα μοιάζει με αυτήν: = 1,5/1.
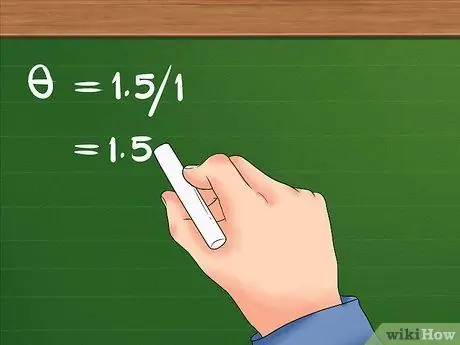
Βήμα 3. Χωρίστε τη γραμμική μετατόπιση με την ακτίνα
Αυτή η διαίρεση θα έχει ως αποτέλεσμα τη γωνιακή μετατόπιση του αντικειμένου.
- Αφού διαιρέσουμε το 1,5 με το 1, το αποτέλεσμα είναι 1.5. Η γωνιακή μετατόπιση του κοριτσιού είναι 1,5 ακτίνια.
- Δεδομένου ότι η γωνιακή μετατόπιση μετρά πόσο περιστρέφεται ένα αντικείμενο από την αρχική του θέση, θα πρέπει να μετράται ως γωνία και όχι ως απόσταση. Το ακτίνιο είναι η μονάδα που χρησιμοποιείται για τη μέτρηση γωνιών.
Μέρος 5 από 5: Κατανόηση για τη μετανάστευση
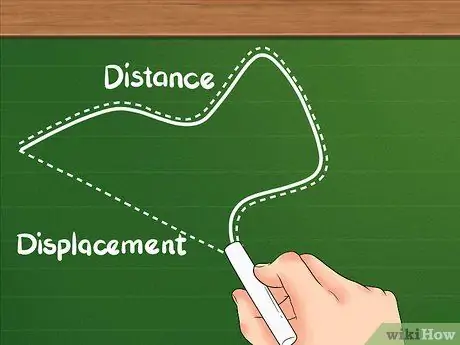
Βήμα 1. Γνωρίστε ότι η απόσταση έχει διαφορετικό ορισμό από τη μετατόπιση
Η απόσταση δείχνει πόσο μακριά είναι η συνολική απόσταση που διανύει το αντικείμενο.
- Η απόσταση είναι συχνά γνωστή ως κλιμακωτή ποσότητα. Η απόσταση δείχνει την απόσταση που διανύει ένα αντικείμενο ανεξάρτητα από την κατεύθυνση του αντικειμένου.
- Για παράδειγμα, αν περπατήσετε 2 βήματα ανατολικά, 2 βήματα νότια, 2 βήματα δυτικά και στη συνέχεια 2 βήματα βόρεια, θα επιστρέψετε στην αρχική σας θέση. Ακόμα κι αν έχετε περάσει από το σύνολο απόσταση 10 βήματα μακριά, απλά κίνηση 0 βήματα μακριά επειδή η τελική τοποθεσία σας είναι ίδια με την τοποθεσία εκκίνησης (η διαδρομή σας μοιάζει με πλαίσιο).

Βήμα 2. Κατανοήστε ότι η μετατόπιση είναι η διαφορά μεταξύ δύο τοποθεσιών
Η μετατόπιση δεν είναι το συνολικό άθροισμα της κίνησης όπως η απόσταση. μετατοπίζει την εστίαση στην περιοχή μεταξύ των τοποθεσιών έναρξης και λήξης.
- Η μετατόπιση ονομάζεται διανυσματικό μέγεθος και δείχνει την αλλαγή στη θέση ενός αντικειμένου λαμβάνοντας υπόψη την κατεύθυνση κίνησης του αντικειμένου.
- Για παράδειγμα, περπατάτε ανατολικά για 5 βήματα. Αν γυρίσετε δυτικά 5 σκαλιά, θα κινηθείτε προς την αντίθετη κατεύθυνση από την αρχική σας τοποθεσία. Παρόλο που έχετε καλύψει 10 βήματα, η θέση σας δεν έχει αλλάξει. η μετατόπιση σας είναι 0 βήματα.

Βήμα 3. Θυμηθείτε τις λέξεις μπροστά και πίσω όταν προσπαθείτε να φανταστείτε μετατόπιση
Η κίνηση προς την αντίθετη κατεύθυνση εξαλείφει τη μετατόπιση ενός αντικειμένου.
Φανταστείτε έναν προπονητή ποδοσφαίρου μπρος -πίσω στο περιθώριο. Καθώς φώναζε στους παίκτες, άλλαξε από αριστερά προς τα δεξιά αρκετές φορές. Αν τον παρακολουθείτε καθώς κινείται από αριστερά προς τα δεξιά, παρατηρείτε τη συνολική απόσταση που έχει διανύσει. Ωστόσο, ας υποθέσουμε ότι ο προπονητής σταματά να μιλάει με τον άμυνα στο πλάι. Εάν βρίσκεται σε διαφορετικό σημείο από την αρχική του θέση πριν μετακινηθεί, τότε παρατηρείτε την κίνηση του εκπαιδευτή

Βήμα 4. Γνωρίστε ότι η μετατόπιση μετριέται χρησιμοποιώντας μια ευθεία διαδρομή και όχι μια κυκλική διαδρομή
Για να βρείτε μετατόπιση, πρέπει να βρείτε τον συντομότερο και αποδοτικότερο τρόπο για να υπολογίσετε τη διαφορά μεταξύ δύο σημείων.
- Μια κυκλική διαδρομή θα σας μεταφέρει από την τοποθεσία εκκίνησης στην τελική σας τοποθεσία, αλλά δεν είναι η συντομότερη διαδρομή. Για να σας βοηθήσουμε να το απεικονίσετε, φανταστείτε ότι περπατάτε σε ευθεία γραμμή και συναντάτε έναν πυλώνα. Δεν μπορείτε να σπάσετε αυτόν τον πυλώνα, οπότε περιστρέψτε τον. Παρόλο που η τελική σας θέση είναι η ίδια με την περίπτωση που σπάσατε τον πυλώνα, θα χρειαστείτε επιπλέον βήματα για να επιτύχετε αυτόν τον στόχο.
- Παρόλο που η μετατόπιση αντιπροσωπεύει μια ευθεία διαδρομή, γνωρίζετε ότι μπορείτε να μετρήσετε τη μετατόπιση ενός αντικειμένου που είναι επί του παρόντος κινούνται σε κυκλική διαδρομή. Αυτή η μετατόπιση ονομάζεται γωνιακή μετατόπιση και μπορεί να υπολογιστεί με την εύρεση της συντομότερης διαδρομής από την αρχική θέση στην τελική θέση.

Βήμα 5. Γνωρίστε ότι η μετατόπιση μπορεί να είναι αρνητική, σε αντίθεση με την απόσταση
Εάν η τελική σας τοποθεσία φτάσει κινούμενη προς την αντίθετη κατεύθυνση προς την αρχική σας κατεύθυνση, τότε η μετατόπιση σας είναι αρνητική.
- Για παράδειγμα, περπατάμε 5 βήματα ανατολικά και μετά 3 βήματα δυτικά. Παρόλο που με υπολογισμό μετακινείστε 2 βήματα από την αρχική σας θέση, η μετατόπιση σας είναι -2 επειδή κινείστε προς την αντίθετη κατεύθυνση. Η απόσταση σας θα είναι πάντα θετική γιατί δεν μπορείτε να μετρήσετε αντίστροφα σε βήματα, χιλιόμετρα κ.ο.κ.
- Η αρνητική μετατόπιση δεν σημαίνει ότι η μετατόπιση μειώνεται. Αρνητικό σημαίνει απλώς ότι η κατεύθυνση είναι αντίθετη.

Βήμα 6. Συνειδητοποιήστε ότι μερικές φορές η απόσταση και η μετατόπιση μπορεί να είναι οι ίδιες
Εάν περπατήσετε ευθεία για 25 βήματα και σταματήσετε, η απόσταση που θα διανύσετε θα είναι ίση με την μετατόπιση από την αρχική σας θέση.
- Αυτό ισχύει μόνο όταν μετακινείστε από μία τοποθεσία από την αρχική σας θέση σε ευθεία γραμμή. Για παράδειγμα, ζείτε στο Σαν Φρανσίσκο της Καλιφόρνια και παίρνετε μια νέα δουλειά στο Λας Βέγκας της Νεβάδα. Πρέπει να μετακομίσετε στο Λας Βέγκας για να είστε κοντά στη δουλειά σας. Αν ανέβεις σε αεροπλάνο που πετάει ευθεία από το Σαν Φρανσίσκο στο Λας Βέγκας, θα διανύσετε την ίδια απόσταση και μετατόπιση x.
- Ωστόσο, εάν οδηγείτε από το Σαν Φρανσίσκο στο Λας Βέγκας, θα διανύσετε μια απόσταση x, αλλά θα διανύσετε μια απόσταση y. Δεδομένου ότι η οδήγηση ενός αυτοκινήτου έχει συνήθως μεταβλητές κατευθύνσεις (ανατολικά αυτού του δρόμου, δυτικά αυτού του δρόμου), θα διανύσετε μεγαλύτερες αποστάσεις από τη μικρότερη απόσταση μεταξύ των δύο πόλεων.






