- Συγγραφέας Jason Gerald gerald@how-what-advice.com.
- Public 2024-01-16 19:20.
- Τελευταία τροποποίηση 2025-01-23 12:15.
Στη μελέτη οπτικών οργάνων, η "μεγέθυνση" ενός αντικειμένου που μοιάζει με φακό είναι η αναλογία του ύψους της εικόνας που βλέπετε προς το πραγματικό ύψος του αντικειμένου. Για παράδειγμα, ένας φακός που μπορεί να κάνει ένα αντικείμενο να φαίνεται πολύ μεγάλο έχει έναν "υψηλό" συντελεστή μεγέθυνσης, ενώ ένας φακός που κάνει ένα αντικείμενο να φαίνεται μικρό έχει έναν "χαμηλό" συντελεστή μεγέθυνσης. Ο τύπος για τη μεγέθυνση ενός αντικειμένου υπολογίζεται συνήθως χρησιμοποιώντας τον τύπο M = (hΕγώ/hο) = -(δΕγώ/ρεο), όπου M = μεγέθυνση, hΕγώ = ύψος εικόνας, hο = ύψος αντικειμένου, και δΕγώ και Δο = απόσταση εικόνας και αντικειμένου.
Βήμα
Μέθοδος 1 από 2: Υπολογισμός μεγέθυνσης ενός φακού
Σημειώσεις: Α συγκλίνων φακών ευρύτερο στο κέντρο παρά στις άκρες (σαν μεγεθυντικός φακός). ένα αποκλίνων φακός ευρύτερο στις άκρες παρά στο κέντρο (σαν μπολ). Ο υπολογισμός της μεγέθυνσης και στους δύο φακούς είναι ο ίδιος, με μια σημαντική εξαίρεση Το Κάντε κλικ εδώ για να μεταβείτε απευθείας στις εξαιρέσεις από διαφορετικούς φακούς.
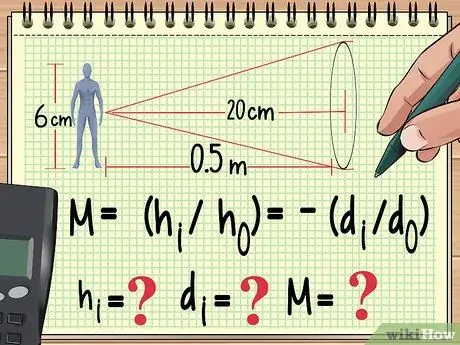
Βήμα 1. Ξεκινήστε με την εξίσωση και τις μεταβλητές που γνωρίζετε ήδη
Όπως κάθε άλλο πρόβλημα φυσικής, ο τρόπος επίλυσης ενός προβλήματος διεύρυνσης είναι να γράψετε την εξίσωση που θα χρησιμοποιήσετε για να τον υπολογίσετε. Από εδώ, μπορείτε να εργαστείτε αντίστροφα για να βρείτε την τιμή της μεταβλητής που δεν έχετε βρει από την εξίσωση που χρησιμοποιείτε.
-
Για παράδειγμα, ας υποθέσουμε ότι μια κούκλα ύψους 6 εκατοστών τοποθετείται ένα μέτρο από το a συγκλίνων φακών με εστιακό μήκος 20 cm. Αν θέλουμε να υπολογίσουμε τη μεγέθυνση, το ύψος της εικόνας και την απόσταση της εικόνας, μπορούμε να αρχίσουμε να γράφουμε την εξίσωση μας ως εξής:
-
- M = (hΕγώ/hο) = -(δΕγώ/ρεο)
-
- Τώρα ξέρουμε hο (ύψος της κούκλας) και δο (απόσταση κούκλας από το φακό). Γνωρίζουμε επίσης το εστιακό μήκος του φακού, το οποίο δεν βρίσκεται σε αυτήν την εξίσωση. Θα μετρήσουμε ηΕγώ, δΕγώ, και Μ.

Βήμα 2. Χρησιμοποιώντας την εξίσωση φακού για να λάβετε το dΕγώ.
Εάν γνωρίζετε την απόσταση από το αντικείμενο που μεγεθύνετε και το εστιακό μήκος του φακού, ο υπολογισμός της απόστασης από την εικόνα που σχηματίζεται είναι πολύ εύκολος με την εξίσωση του φακού. Η εξίσωση του φακού είναι 1/f = 1/dο + 1/ημέραΕγώ, όπου f = εστιακό μήκος του φακού.
-
Σε αυτό το παράδειγμα προβλήματος, μπορούμε να χρησιμοποιήσουμε την εξίσωση φακού για τον υπολογισμό του dΕγώΤο Εισαγάγετε τις τιμές των f και dΕγώ τότε λύστε την εξίσωση:
-
- 1/f = 1/dο + 1/ημέραΕγώ
- 1/20 = 1/50 + 1/ημέραΕγώ
- 5/100 - 2/100 = 1/ημέραΕγώ
- 3/100 = 1/ημέραΕγώ
- 100/3 = δΕγώ = 33,3 εκ
-
- Το εστιακό μήκος του φακού είναι η απόσταση από το κέντρο του φακού έως το σημείο όπου το φως μεταδίδεται στο εστιακό σημείο. Αν έχετε εστιάσει ποτέ το φως με μεγεθυντικό φακό στα καμένα μυρμήγκια, το έχετε δει. Στις ερωτήσεις του μαθήματος, συνήθως δίνεται το μέγεθος αυτού του hotspot. Στην πραγματική ζωή, αυτές οι προδιαγραφές συνήθως γράφονται σε μια ετικέτα που βρίσκεται στον φακό.

Βήμα 3. Υπολογισμός hΕγώ.
Αφού υπολογίσετε το dο και ΔΕγώ, μπορείτε να υπολογίσετε το ύψος του μεγεθυνμένου αντικειμένου και τη μεγέθυνση του φακού. Παρατηρήστε τα δύο σύμβολα ίσων στην εξίσωση μεγέθυνσης φακού (M = (hΕγώ/hο) = -(δΕγώ/ρεο)) - αυτό σημαίνει ότι όλα τα μέρη αυτής της εξίσωσης είναι ίσα μεταξύ τους, οπότε μπορούμε να υπολογίσουμε τα M και hΕγώ με όποια σειρά θέλουμε.
-
Για αυτό το παράδειγμα προβλήματος, μπορούμε να υπολογίσουμε το hΕγώ σαν αυτό:
-
- (ηΕγώ/hο) = -(δΕγώ/ρεο)
- (ηΕγώ/6) = -(33, 3/50)
- ηΕγώ = -(33, 3/50) x 6
- ηΕγώ = - 3, 996 εκ
-
- Σημειώστε ότι το ύψος του αντικειμένου εδώ είναι αρνητικό, γεγονός που υποδηλώνει ότι η εικόνα που θα δούμε αργότερα θα αντιστραφεί (πάνω-κάτω).

Βήμα 4. Υπολογισμός Μ
Μπορείτε να υπολογίσετε την τελευταία μεταβλητή με την εξίσωση -(δΕγώ/ρεο) ή (ηΕγώ/hο).
-
Στο παρακάτω παράδειγμα, ο τρόπος υπολογισμού του Μ είναι ο εξής:
-
- M = (hΕγώ/hο)
-
Μ = (-3, 996/6) = - 0, 666
-
-
Το αποτέλεσμα θα είναι επίσης το ίδιο όταν υπολογίζεται χρησιμοποιώντας την τιμή d:
-
- Μ = -(δΕγώ/ρεο)
- Μ = -(33, 3/50) = - 0, 666
-
- Σημειώστε ότι το ζουμ δεν έχει ετικέτα μονάδας.
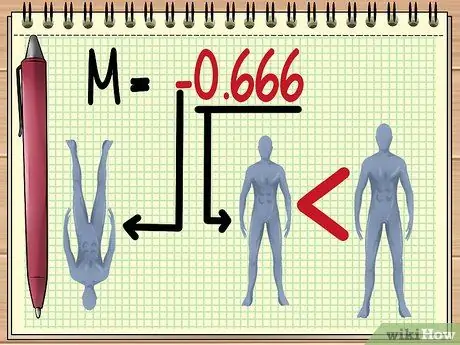
Βήμα 5. Κατανόηση της τιμής Μ
Μόλις λάβετε το μέγεθος της τιμής Μ, μπορείτε να εκτιμήσετε πολλά πράγματα για την εικόνα που θα δείτε μέσα από το φακό, και συγκεκριμένα:
-
Το μέγεθος.
Όσο μεγαλύτερη είναι η "απόλυτη τιμή" του Μ, τόσο μεγαλύτερο θα εμφανίζεται το αντικείμενο που φαίνεται με το φακό. Η τιμή M μεταξύ 0 και 1 υποδηλώνει ότι το αντικείμενο θα φαίνεται μικρότερο.
-
Αντικειμενικός προσανατολισμός.
Μια αρνητική τιμή υποδεικνύει ότι η εικόνα που σχηματίζεται θα αντιστραφεί.
- Στο παράδειγμα που δίνεται εδώ, η τιμή Μ -0,666 σημαίνει ότι, σύμφωνα με την τιμή της υπάρχουσας μεταβλητής, η σκιά της κούκλας θα είναι ορατή. ανάποδα και δύο τρίτα μικρότερα από το πραγματικό μέγεθος.
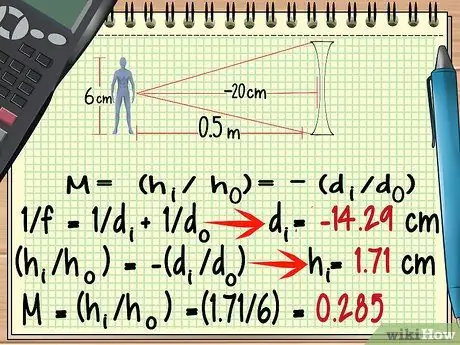
Βήμα 6. Για αποκλίνοντες φακούς, χρησιμοποιήστε ένα αρνητικό εστιακό σημείο
Αν και το σχήμα ενός αποκλίνοντος φακού είναι πολύ διαφορετικό από αυτό ενός συγκλίνοντος φακού, μπορείτε να υπολογίσετε τη μεγέθυνσή του χρησιμοποιώντας τον ίδιο τύπο όπως παραπάνω. Οι εξαιρέσεις που πρέπει να θυμάστε είναι Το σημείο εστίασης του αποκλίνοντος φακού είναι αρνητικό.
Στο παραπάνω παράδειγμα του προβλήματος, αυτό θα επηρεάσει την απάντηση που θα λάβετε στον υπολογισμό του dΕγώ, οπότε φροντίστε να δώσετε προσοχή σε αυτό.
-
Ας ξαναδουλέψουμε το παραπάνω παράδειγμα παραδείγματος, μόνο που τώρα χρησιμοποιούμε αποκλίνοντες φακούς με εστιακή απόσταση - 20 εκ.
Οι άλλες μεταβλητές παραμένουν στην ίδια τιμή.
-
Πρώτα απ 'όλα, θα υπολογίσουμε το dΕγώ χρησιμοποιώντας την εξίσωση φακού:
-
- 1/f = 1/dο + 1/ημέραΕγώ
- 1/-20 = 1/50 + 1/ημέραΕγώ
- -5/100 - 2/100 = 1/ημέραΕγώ
- -7/100 = 1/ημέραΕγώ
- -100/7 = δΕγώ = - 14, 29 εκ
-
-
Τώρα θα υπολογίσουμε το hΕγώ και Μ με τιμή dΕγώ το καινουργιο.
-
- (ηΕγώ/hο) = -(δΕγώ/ρεο)
- (ηΕγώ/6) = -(-14, 29/50)
- ηΕγώ = -(- -14, 29/50) x 6
- ηΕγώ = 1, 71 εκ
- M = (hΕγώ/hο)
- Μ = (1, 71/6) = 0, 285
-
Μέθοδος 2 από 2: Υπολογισμός της μεγέθυνσης πολλαπλών φακών
Απλή μέθοδος δύο φακών
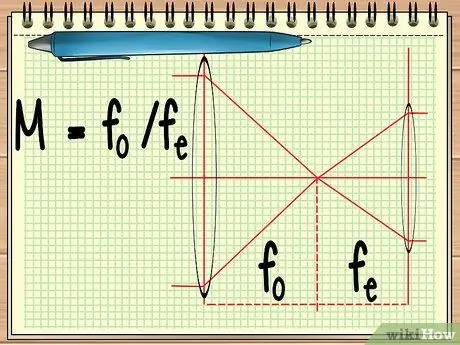
Βήμα 1. Υπολογίστε το εστιακό σημείο των δύο φακών
Όταν χρησιμοποιείτε ένα όργανο που αποτελείται από δύο φακούς τοποθετημένους δίπλα -δίπλα (όπως ένα τηλεσκόπιο ή ένα ζευγάρι κιάλια), το μόνο που πρέπει να μάθετε είναι το εστιακό σημείο των δύο φακών για να υπολογίσετε τη συνολική μεγέθυνση των δύο φακών. αυτό μπορεί να υπολογιστεί με την απλή εξίσωση M = fο/φάμι.
Στην εξίσωση, fο είναι το εστιακό σημείο του αντικειμενικού φακού και fμι είναι το κεντρικό σημείο του προσοφθάλμιου φακού. Ο αντικειμενικός φακός είναι ο μεγάλος φακός που βρίσκεται κοντά στο αντικείμενο, ενώ ο οφθαλμικός φακός είναι ο φακός που βρίσκεται κοντά στο μάτι του παρατηρητή.

Βήμα 2. Συνδέστε τις πληροφορίες που έχετε ήδη στην εξίσωση M = fο/φάμι.
Μόλις έχετε τα εστιακά σημεία και των δύο φακών, είναι πολύ εύκολο να τα υπολογίσετε, - υπολογίστε την αναλογία διαιρώντας το εστιακό μήκος του αντικειμενικού φακού με το εστιακό μήκος του προσοφθάλμιου φακού. Η απάντηση που παίρνετε είναι η συνολική μεγέθυνση του εργαλείου.
-
Για παράδειγμα, ας υποθέσουμε ένα απλό τηλεσκόπιο, γράφεται ότι το εστιακό σημείο του αντικειμενικού φακού είναι 10cm και το εστιακό σημείο του προσοφθάλμιου φακού είναι 5cm, τότε η μεγέθυνση είναι 10/5 = 2.
Πολύπλοκη μέθοδος
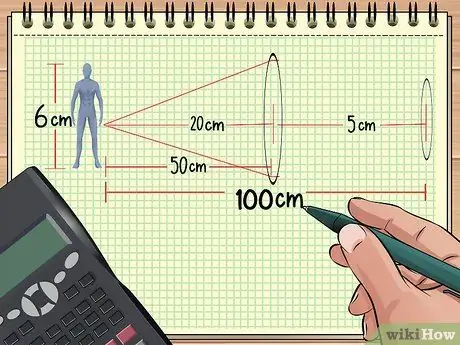
Υπολογισμός μεγέθυνσης Βήμα 9 Βήμα 1. Υπολογίστε την απόσταση μεταξύ των φακών και του αντικειμένου
Εάν έχετε δύο φακούς διατεταγμένους στη σειρά μπροστά από ένα αντικείμενο, η συνολική μεγέθυνση μπορεί να υπολογιστεί εάν γνωρίζετε την απόσταση από τους φακούς στο αντικείμενο, το μέγεθος του αντικειμένου και το εστιακό σημείο των δύο φακών. Το υπόλοιπο μπορεί επίσης να υπολογιστεί.
Για παράδειγμα, ας υποθέσουμε ότι τακτοποιούμε αντικείμενα και φακούς όπως στο πρόβλημα 1 παραπάνω: μια κούκλα απέχει 50 cm από έναν συγκλίνοντα φακό που έχει εστιακό μήκος 20 cm. Τώρα, τοποθετήστε τον δεύτερο φακό με εστιακό σημείο 5 cm σε απόσταση 50 cm από τον πρώτο φακό (100 cm από την κούκλα.) Μετά από αυτό, θα υπολογίσουμε τη συνολική μεγέθυνση χρησιμοποιώντας τις πληροφορίες που έχουμε λάβει
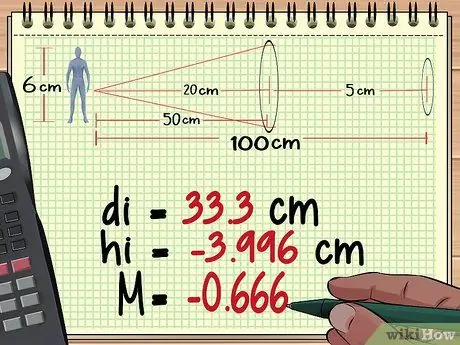
Υπολογίστε Βήμα 10 μεγέθυνσης Βήμα 2. Υπολογίστε την απόσταση, το ύψος και τη μεγέθυνση του αντικειμένου από τον φακό 1
Το πρώτο μέρος του υπολογισμού της μεγέθυνσης πολλαπλών φακών είναι το ίδιο με τον υπολογισμό της μεγέθυνσης ενός φακού. Ξεκινήστε με τον φακό που βρίσκεται πιο κοντά στο αντικείμενο, χρησιμοποιήστε την εξίσωση φακού για να βρείτε την απόσταση από τη σχηματιζόμενη εικόνα και, στη συνέχεια, χρησιμοποιήστε την εξίσωση μεγέθυνσης για να βρείτε το ύψος και τη μεγέθυνση της εικόνας. Κάντε κλικ εδώ για να δείτε περισσότερους υπολογισμούς μεγέθυνσης φακού.
-
Από τους υπολογισμούς μας στη Μέθοδο 1 παραπάνω, διαπιστώνουμε ότι ο πρώτος φακός παράγει μια εικόνα τόσο υψηλή όσο - 3, 996 εκ, απόσταση 33,3 εκ πίσω από το φακό και σε μεγέθυνση - 0, 666.
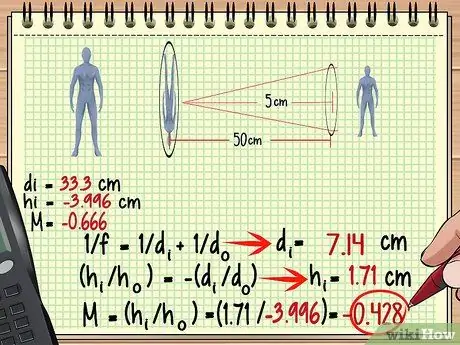
Υπολογισμός μεγέθυνσης Βήμα 11 Βήμα 3. Χρησιμοποιήστε την εικόνα από τον πρώτο φακό ως αντικείμενο από τον δεύτερο φακό
Τώρα, η εύρεση της μεγέθυνσης, του ύψους και άλλων για τον δεύτερο φακό είναι πολύ εύκολη - απλώς χρησιμοποιήστε την ίδια μέθοδο που χρησιμοποιήσατε για τον πρώτο φακό, μόνο αυτή τη φορά αντιμετωπίστε την εικόνα ως αντικείμενο. Θυμηθείτε ότι η απόσταση εικόνας από τον δεύτερο φακό δεν είναι πάντα η ίδια με την απόσταση του αντικειμένου από τον πρώτο φακό.
-
Στο παραπάνω παράδειγμα, δεδομένου ότι η εικόνα σχηματίζεται 33,3 cm πίσω από τον πρώτο φακό, η απόσταση είναι 50-33,3 = 16,7 εκ μπροστά στον δεύτερο φακό. Ας χρησιμοποιήσουμε αυτήν τη μέτρηση και το εστιακό μήκος του δεύτερου φακού για να βρούμε την εικόνα που σχηματίζεται από τον δεύτερο φακό.
-
- 1/f = 1/dο + 1/ημέραΕγώ
- 1/5 = 1/16, 7 + 1/ημέραΕγώ
- 0, 2 - 0, 0599 = 1/ημέραΕγώ
- 0, 14 = 1/ημέραΕγώ
- ρεΕγώ = 7, 14 εκ
-
-
Τώρα μπορούμε να υπολογίσουμε το hΕγώ και Μ για τον δεύτερο φακό:
-
- (ηΕγώ/hο) = -(δΕγώ/ρεο)
- (ηΕγώ/-3, 996) = -(7, 14/16, 7)
- ηΕγώ = -(0, 427) χ -3, 996
- ηΕγώ = 1, 71 εκ
- M = (hΕγώ/hο)
- Μ = (1, 71/-3, 996) = - 0, 428
-
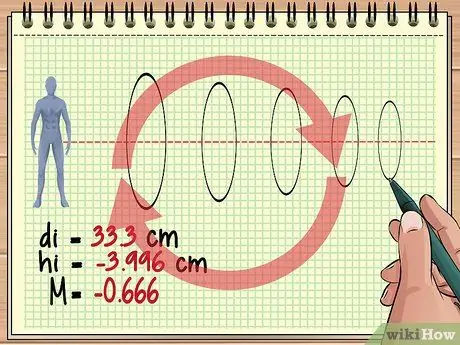
Υπολογίστε Βήμα 12 μεγέθυνσης Βήμα 4. Συνεχίστε τον υπολογισμό έτσι για τους επιπλέον φακούς
Αυτή η βασική προσέγγιση είναι η ίδια εάν υπάρχουν τρεις, τέσσερις ή εκατοντάδες φακοί ευθυγραμμισμένοι μπροστά από ένα αντικείμενο. Για κάθε φακό, θεωρήστε την εικόνα του προηγούμενου φακού ως αντικείμενο και χρησιμοποιήστε την εξίσωση φακού και την εξίσωση μεγέθυνσης για να βρείτε την απάντηση που θέλετε.
Λάβετε υπόψη ότι κάθε επόμενος φακός μπορεί να αναστρέφει συνεχώς την εικόνα που σχηματίζεται. Για παράδειγμα, η τιμή μεγέθυνσης που λάβαμε νωρίτερα (-0, 428) υποδηλώνει ότι η εικόνα που πρόκειται να δούμε είναι περίπου 4/10 του πραγματικού μεγέθους αντικειμένου, αλλά κάθετη, επειδή η εικόνα από τον προηγούμενο φακό είναι ανεστραμμένη
Συμβουλές
- Τα κιάλια παρέχουν συνήθως μια εξήγηση των προδιαγραφών μεγέθυνσης με τη μορφή αριθμού πολλαπλασιασμού ενός άλλου αριθμού. Για παράδειγμα, τα κιάλια μπορούν να οριστούν ως 8x25 ή 8x40. Όταν γράφεται έτσι, ο πρώτος αριθμός είναι η μεγέθυνση των διόπτρων. Δεν έχει σημασία ακόμη και αν στο παράδειγμα που δόθηκε, οι δύο αριθμοί είναι διαφορετικοί σε μέγεθος, και τα δύο κιάλια έχουν μεγέθυνση 8 φορές. Ο δεύτερος αριθμός υποδεικνύει πόσο καθαρή θα σχηματιστεί η εικόνα από τα κιάλια.
- Θυμηθείτε ότι για τη λούπα ενός φακού, η μεγέθυνση θα είναι αρνητική εάν η απόσταση του αντικειμένου είναι μεγαλύτερη από την εστιακή απόσταση του φακού. Αυτό δεν σημαίνει ότι η εικόνα που σχηματίζεται θα είναι μικρότερη. Σε αυτήν την περίπτωση, η μεγέθυνση εξακολουθεί να συμβαίνει, αλλά η εικόνα που σχηματίζεται θα φαίνεται ανάποδα (από πάνω προς τα κάτω) από τον παρατηρητή.
-






