Το αμοιβαίο ή το αμοιβαίο είναι πολύ χρήσιμο σε όλα τα είδη αλγεβρικών εξισώσεων. Για παράδειγμα, όταν διαιρείτε ένα κλάσμα με ένα άλλο, πολλαπλασιάζετε το πρώτο κλάσμα με το αντίστροφο του δεύτερου. Πρέπει επίσης να χρησιμοποιήσετε το αντίστροφο όταν ψάχνετε για την εξίσωση μιας γραμμής.
Βήμα
Μέθοδος 1 από 3: Εύρεση του αντίστροφου ενός κλάσματος ή ενός ακέραιου
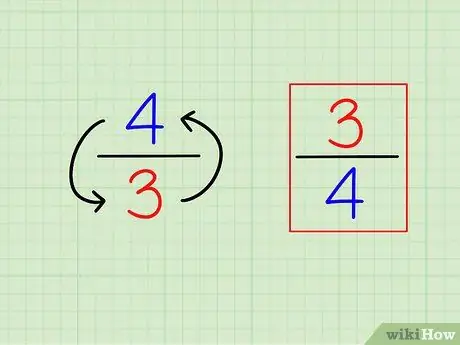
Βήμα 1. Βρείτε το αντίστροφο του κλάσματος αντιστρέφοντάς το
Ο ορισμός του «αμοιβαίου» ή του αντίθετου είναι πολύ εύκολος. Για να βρείτε το αντίστροφο οποιουδήποτε ακέραιου αριθμού, απλώς υπολογίστε το "1 (αυτός ο αριθμός)". Για τα κλάσματα, το αντίστροφο είναι διαφορετικό κλάσμα, δηλαδή οι αριθμοί είναι "ανεστραμμένοι" (αντίστροφο).
- Για παράδειγμα, το αντίθετο του 3/4 είναι 4/3.
- Οποιοσδήποτε αριθμός πολλαπλασιάζεται με τις αμοιβαίες αποδόσεις 1.
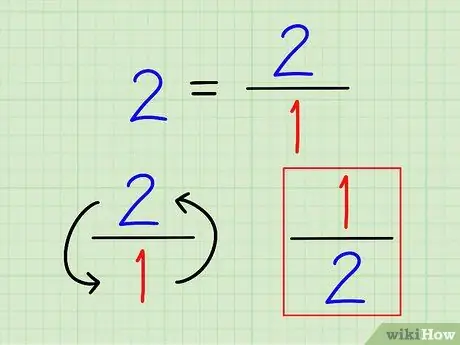
Βήμα 2. Γράψτε το αντίστροφο του ακέραιου αριθμού ως κλάσμα
Και πάλι, το αντίστροφο ενός αριθμού είναι πάντα 1 (αυτός ο αριθμός). Για ακέραιους αριθμούς, γράψτε τους ως κλάσματα. Δεν έχει νόημα ο υπολογισμός αυτού του αριθμού σε δεκαδικό.
Για παράδειγμα, το αντίστροφο του 2 είναι 1 2 = 1/2.
Μέθοδος 2 από 3: Εύρεση του αντίστροφου ενός μικτού κλάσματος
Βήμα 1. Προσδιορίστε μικτούς αριθμούς
Τα μικτά κλάσματα αποτελούνται από ακέραιους αριθμούς και κλάσματα, όπως 24/5Το Υπάρχουν δύο βήματα για να βρεθεί το αντίστροφο ενός μικτού αριθμού όπως περιγράφεται παρακάτω.
Βήμα 2. Μετατρέψτε μικτούς αριθμούς σε ακατάλληλα κλάσματα
Να θυμάστε ότι το 1 μπορεί πάντα να γραφτεί ως (αριθμός)/(ίδιος αριθμός) και τα κλάσματα με τον ίδιο παρονομαστή (κάτω αριθμός) μπορούν να προστεθούν μαζί. Εδώ είναι ένα παράδειγμα που χρησιμοποιεί το 24/5:
- 24/5
- = 1 + 1 + 4/5
- = 5/5 + 5/5 + 4/5
- = (5+5+4)/5
- = 14/5.
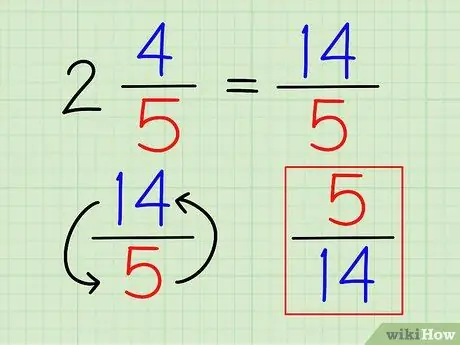
Βήμα 3. Αναποδογυρίστε το κλάσμα
Μόλις ο αριθμός γραφτεί εντελώς ως κλάσμα, μπορείτε να βρείτε το αμοιβαίο του όπως ακριβώς θα κάνατε σε οποιοδήποτε άλλο κλάσμα, αντιστρέφοντας το κλάσμα.
Στο παραπάνω παράδειγμα, το αμοιβαίο των 14/5 είναι 5/14.
Μέθοδος 3 από 3: Εύρεση του αντίθετου ενός δεκαδικού
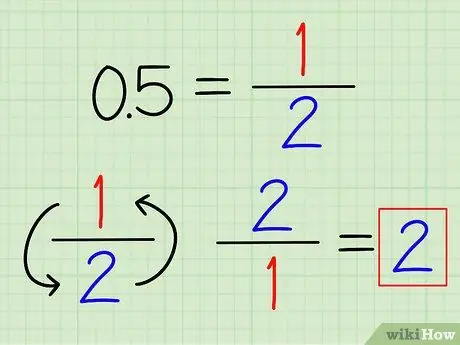
Βήμα 1. Μετατρέψτε τα δεκαδικά σε κλάσματα, αν είναι δυνατόν
Μπορεί να αναγνωρίσετε μερικούς δεκαδικούς αριθμούς που χρησιμοποιούνται συχνά, οι οποίοι μπορούν εύκολα να μετατραπούν σε κλάσματα. Για παράδειγμα, 0,5 = 1/2 και 0,25 = 1/4Το Μόλις το δεκαδικό έχει μετατραπεί σε κλάσμα, απλώς αναποδογυρίστε το κλάσμα για να βρείτε το αντίστροφο.
Για παράδειγμα, το αντίστροφο του 0,5 είναι 2/1 = 2.
Βήμα 2. Γράψτε πρόβλημα διαίρεσης
Εάν δεν μπορείτε να το μετατρέψετε σε κλάσμα, υπολογίστε το αντίστροφο του αριθμού με τη μορφή προβλήματος διαίρεσης: 1 (δεκαδικό). Μπορείτε να χρησιμοποιήσετε μια αριθμομηχανή για να το λύσετε ή να προχωρήσετε στο επόμενο βήμα για να το λύσετε με μη αυτόματο τρόπο.
Για παράδειγμα, μπορείτε να βρείτε το αντίστροφο του 0,4 υπολογίζοντας το 1 0,4
Βήμα 3. Αλλάξτε το πρόβλημα διαίρεσης για να χρησιμοποιήσετε ακέραιους αριθμούς
Το πρώτο βήμα για τη διαίρεση των δεκαδικών είναι να μετακινήσετε το δεκαδικό σημείο έως ότου όλοι οι αριθμοί είναι ακέραιοι αριθμοί. Εφόσον μετακινήσετε το δεκαδικό ψηφίο και των δύο αριθμών κατά τον ίδιο αριθμό βημάτων, θα λάβετε τη σωστή απάντηση.
Για παράδειγμα, μπορείτε να χρησιμοποιήσετε το 1 0, 4 και να το ξαναγράψετε ως 10 4. Σε αυτήν την περίπτωση, μετακινείτε όλα τα δεκαδικά ψηφία ένα βήμα προς τα δεξιά, με τον ίδιο τρόπο που πολλαπλασιάζετε κάθε αριθμό με δέκα
Βήμα 4. Λύστε το πρόβλημα χρησιμοποιώντας μακρά διαίρεση
Χρησιμοποιήστε τη μέθοδο της μακράς διαίρεσης για να υπολογίσετε το αμοιβαίο. Αν μετράτε 10 4, θα λάβετε την απάντηση 2, 5 που είναι το αντίστροφο του 0, 4.
Συμβουλές
- Το αρνητικό αντίστροφο ενός αριθμού είναι το ίδιο με το κανονικό αμοιβαίο, αφού πολλαπλασιάζεται με αρνητικό. Για παράδειγμα, η αρνητική αμοιβαία του 3/4 είναι -4/3.
- Το αμοιβαίο ή το αμοιβαίο αναφέρεται συχνά ως "αντίστροφος πολλαπλασιασμός".
- Ο αριθμός 1 είναι το αντίθετο του εαυτού του γιατί 1 1 = 1.
- Ο αριθμός 0 δεν έχει αμφίδρομο γιατί το 0 είναι απροσδιόριστο.
