- Συγγραφέας Jason Gerald gerald@how-what-advice.com.
- Public 2023-12-16 11:05.
- Τελευταία τροποποίηση 2025-01-23 12:15.
Για τους περισσότερους ανθρώπους, τα κλάσματα είναι οι πρώτοι περίπλοκοι υπολογισμοί που συναντήθηκαν. Η έννοια των κλασμάτων είναι αρκετά δύσκολη και απαιτεί να μάθετε ειδικές συνθήκες για να το κάνετε. Επειδή τα κλάσματα έχουν ειδικούς κανόνες για πρόσθεση, αφαίρεση, πολλαπλασιασμό και διαίρεση, πολλοί άνθρωποι μπερδεύονται με αυτό. Ωστόσο, με πολλή εξάσκηση, ο καθένας μπορεί να μάθει και να ολοκληρώσει υπολογισμούς που σχετίζονται με κλάσματα.
Βήμα
Μέθοδος 1 από 5: Κατανόηση των κλασμάτων
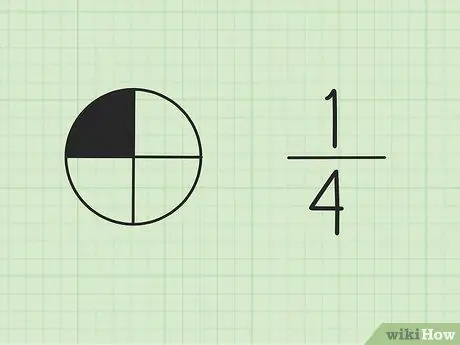
Βήμα 1. Κατανοήστε ότι τα κλάσματα αποτελούν μέρος ενός συνόλου
Ο αριθμός στην κορυφή ονομάζεται αριθμητής και αντιπροσωπεύει τον αριθμό των τμημάτων του συνόλου. Ο αριθμός στο κάτω μέρος ονομάζεται παρονομαστής, ο οποίος αντιπροσωπεύει τον συνολικό αριθμό τμημάτων.
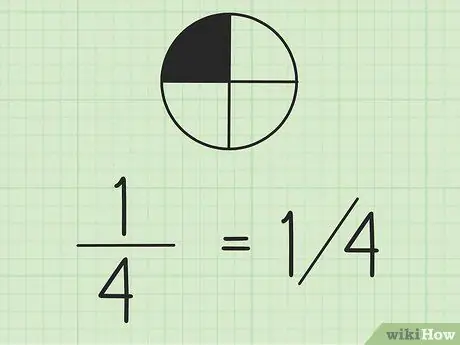
Βήμα 2. Λάβετε υπόψη ότι μπορείτε να γράψετε κλάσματα χρησιμοποιώντας παύλες
Ο αριθμός στα αριστερά είναι ο αριθμητής και ο αριθμός στα δεξιά είναι ο παρονομαστής. Εάν εργάζεστε με κλάσματα στην ίδια ευθεία, είναι καλή ιδέα να γράψετε τον αριθμητή πάνω από τον παρονομαστή.
Για παράδειγμα, αν πάρετε μία από τις τέσσερις φέτες πίτσας, έχετε πίτσα. Αν έχετε 7/3 πίτσες, αυτό σημαίνει ότι έχετε δύο ολόκληρες πίτσες συν 1 από 3 φέτες πίτσας
Μέθοδος 2 από 5: Διαφορά μεταξύ μικτών και απλών κλασμάτων

Βήμα 1. Κατανοήστε ότι οι μεικτοί αριθμοί αποτελούνται από ακέραιους αριθμούς και κλάσματα, για παράδειγμα 2 1/3 ή 45 1/2
Συνήθως, πρέπει να μετατρέψετε μικτούς αριθμούς σε απλούστερη μορφή για να προσθέσετε, να αφαιρέσετε, να πολλαπλασιάσετε ή να διαιρέσετε.

Βήμα 2. Αλλάξτε τον μεικτό αριθμό πολλαπλασιάζοντας ολόκληρο τον αριθμό με τον παρονομαστή στο κλάσμα και, στη συνέχεια, προσθέτοντάς τον με τον αριθμητή
Γράψτε το αποτέλεσμα ως αριθμητή, ενώ ο παρονομαστής δεν αλλάζει.
Για παράδειγμα, για να μετατρέψετε το 2 1/3 σε απλό κλάσμα, πολλαπλασιάστε το 2 επί 3, στη συνέχεια προσθέστε το 1 και λάβετε το 7/3

Βήμα 3. Μετατρέψτε απλά κλάσματα σε μικτούς αριθμούς διαιρώντας τον αριθμητή με τον παρονομαστή
Το σύνολο του αποτελέσματος της διαίρεσης γράφεται ως ακέραιος αριθμός και το υπόλοιπο της διαίρεσης γράφεται ως αριθμητής του κλάσματος. Ο παρονομαστής δεν αλλάζει.
Για παράδειγμα, για να μετατρέψετε το 7/3 σε μικτό αριθμό, διαιρέστε το 7 με το 3 για να πάρετε 2 με το υπόλοιπο 1. Άρα ο μικτός αριθμός είναι 2 1/3. Τα απλά κλάσματα μπορούν να μετατραπούν σε μικτούς αριθμούς μόνο εάν ο αριθμητής είναι μεγαλύτερος από τον παρονομαστή
Μέθοδος 3 από 5: Προσθήκη και αφαίρεση κλασμάτων
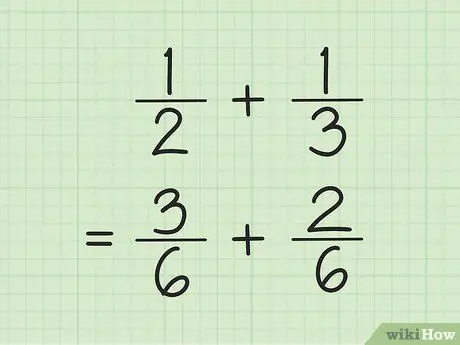
Βήμα 1. Βρείτε έναν κοινό παρονομαστή για να προσθέσετε και να αφαιρέσετε κλάσματα
Το κόλπο, πολλαπλασιάστε τους αριθμούς στον παρονομαστή, στη συνέχεια πολλαπλασιάστε κάθε αριθμητή με τον αριθμό που χρησιμοποιείται για την εύρεση του παρονομαστή. Μερικές φορές, μπορείτε να βρείτε το LCM (τουλάχιστον κοινό πολλαπλάσιο) για τον παρονομαστή πολλαπλασιάζοντας τους παρονομαστές μεταξύ τους.
Για παράδειγμα, για να προσθέσετε και το 1/3, βρείτε πρώτα το LCM (το λιγότερο κοινό πολλαπλάσιο) των δύο παρονομαστών πολλαπλασιάζοντας το ένα το άλλο. Έτσι, πολλαπλασιάζετε 2 και 3 για να πάρετε το LCM 6. Πολλαπλασιάστε το 1 με το 3 για να πάρετε το 3 ως νέο αριθμητή του πρώτου κλάσματος. Πολλαπλασιάστε 1 επί 2 για να πάρετε το 2 ως νέο αριθμητή του δεύτερου κλάσματος. Τα νέα κλάσματά σας είναι 3/6 και 2/6
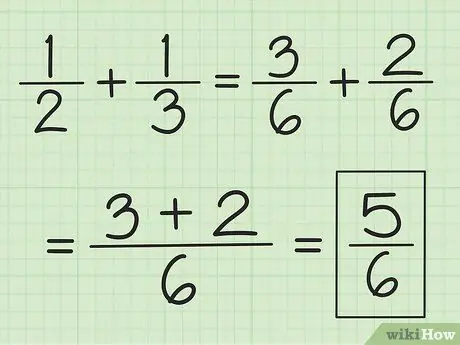
Βήμα 2. Προσθέστε τους δύο αριθμητές μαζί και μην αλλάξετε τον παρονομαστή
Για παράδειγμα, 3/6 συν 2/6 είναι 5/6 και 2/6 συν 1/6 είναι 3/6
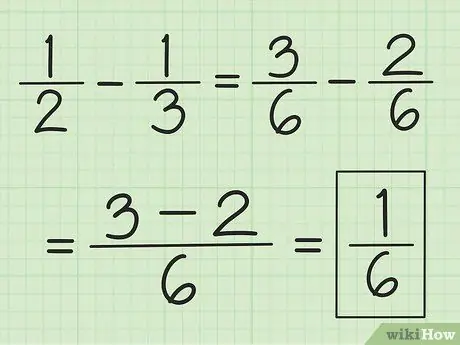
Βήμα 3. Χρησιμοποιήστε μια παρόμοια τεχνική για αφαίρεση
Βρείτε πρώτα το LCM των παρονομαστών, αλλά αντί να τα προσθέσετε, αφαιρέστε τον αριθμό του πρώτου αριθμητή από τον αριθμό του δεύτερου.
Για παράδειγμα, για να αφαιρέσετε το 1/3 από το 1/2, αλλάξτε πρώτα τα κλάσματα σε 3/6 και 2/6, στη συνέχεια αφαιρέστε το 3 επί 2 για να πάρετε 1. Αυτό έχει ως αποτέλεσμα το 1/6
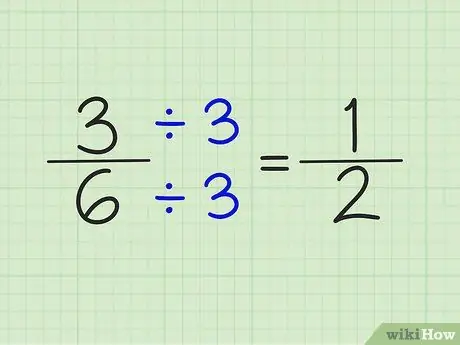
Βήμα 4. Απλοποιήστε τα κλάσματα διαιρώντας τον αριθμητή και τον παρονομαστή με τον ίδιο αριθμό
Για παράδειγμα, ο αριθμός 5/6 δεν μπορεί να απλοποιηθεί. Ωστόσο, το 3/6 μπορεί να απλοποιηθεί διαιρώντας τον αριθμητή και τον παρονομαστή με τον αριθμό 3. Το αποτέλεσμα είναι κλάσμα 1/2

Βήμα 5. Μετατρέψτε το κλάσμα σε μικτό αριθμό εάν ο αριθμητής είναι μεγαλύτερος από τον παρονομαστή
Μέθοδος 4 από 5: Πολλαπλασιάστε και διαιρέστε κλάσματα
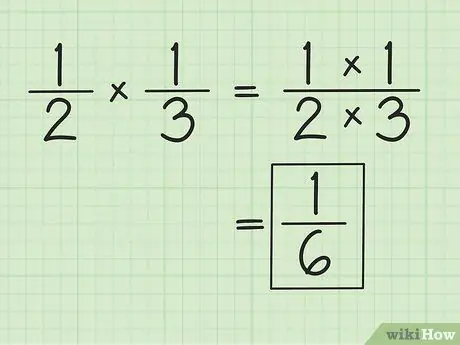
Βήμα 1. Πολλαπλασιάστε τον αριθμητή και τον παρονομαστή ξεχωριστά για να πολλαπλασιάσετε τα κλάσματα
Για παράδειγμα, όταν πολλαπλασιάζουμε και 1/3, το αποτέλεσμα είναι 1/6 (1 φορές 1 και 2 φορές 3). Δεν χρειάζεται να αντιστοιχίσετε τους παρονομαστές όταν πολλαπλασιάζετε κλάσματα. Απλοποιήστε ή τροποποιήστε τα αποτελέσματα που λαμβάνονται, εάν είναι απαραίτητο
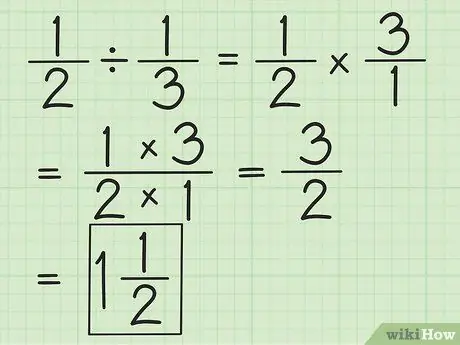
Βήμα 2. Διαιρέστε δύο κλάσματα αντιστρέφοντας το δεύτερο κλάσμα και στη συνέχεια πολλαπλασιάστε και τα δύο
Για παράδειγμα, εάν θέλετε να διαιρέσετε το 1/2 με το 1/3, αντιστρέψτε πρώτα το δεύτερο κλάσμα στα 3/1. Πολλαπλασιάστε με 3/1 και λάβετε 3/2. Απλοποιήστε τα κλάσματα ή μετατρέψτε τους σε μικτούς αριθμούς, αν είναι δυνατόν
Μέθοδος 5 από 5: Εργασία με σύνθετα κλάσματα
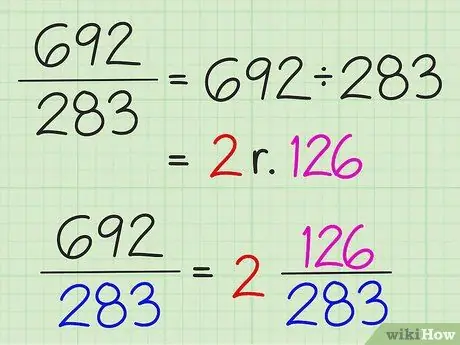
Βήμα 1. Εργαστείτε όλα τα κλάσματα με τον ίδιο τρόπο, ακόμη και αν το πρόβλημα φαίνεται πολύ περίπλοκο
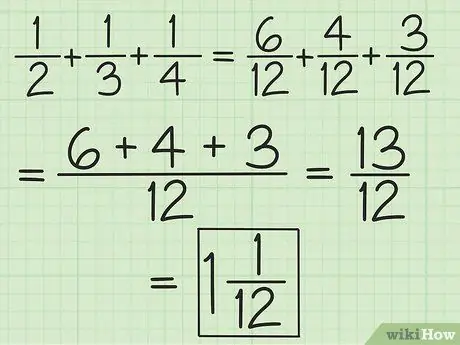
Βήμα 2. Αντιστοιχίστε τους παρονομαστές για όλα τα κλάσματα ή δουλέψτε σε ζεύγη ξεκινώντας από αριστερά προς τα δεξιά για να προσθέσετε και να αφαιρέσετε περισσότερα από δύο κλάσματα
Για παράδειγμα, για να προσθέσετε 1/2, 1/3 και 1/4, μπορείτε να τα αλλάξετε σε 6/12, 4/12 και 3/12 για να λάβετε 13/12 ή μπορείτε να προσθέσετε 3/6 και 2 /6 έτσι παίρνετε 5/6, στη συνέχεια προσθέστε 5/6 και 1/4 (εξισώστε τους παρονομαστές ώστε το δεύτερο κλάσμα να γίνει 3/12) για να πάρετε 13/12 (10/12 συν 3/12). Μετατρέψτε τον σε μεικτό αριθμό, ο οποίος είναι 1 1/12
Συμβουλές
- Θυμηθείτε ότι έχετε μάθει αρκετά μαθηματικά. Τα μαθηματικά είναι σαν μια γλώσσα που μπορείτε να προφέρετε άπταιστα και τώρα προσπαθείτε να μάθετε να το διαβάζετε και να το γράφετε.
- Θυμηθείτε να απλοποιείτε πάντα το τελικό αποτέλεσμα του υπολογισμού σας, είτε το πρόβλημά σας έχει τη μορφή ενός συνηθισμένου κλάσματος, ενός μικτού αριθμού ή ενός σύνθετου κλάσματος.






