- Συγγραφέας Jason Gerald gerald@how-what-advice.com.
- Public 2023-12-16 11:05.
- Τελευταία τροποποίηση 2025-01-23 12:15.
Η προσθήκη κλάσματα είναι μια πολύ χρήσιμη γνώση. Αυτή η δεξιότητα είναι πολύ εύκολη για εκμάθηση και χρήση όταν εργάζεστε σε μαθηματικά προβλήματα από το δημοτικό έως το λύκειο. Αυτό το άρθρο εξηγεί πώς να προσθέσετε κλάσματα, ώστε να μπορείτε να το κάνετε σε λίγα λεπτά.
Βήμα
Μέθοδος 1 από 2: Προσθήκη κλασμάτων με τον ίδιο παρονομαστή

Βήμα 1. Ελέγξτε τον παρονομαστή (τον αριθμό κάτω από το πηλίκο) κάθε κλάσματος
Εάν οι αριθμοί είναι οι ίδιοι, τότε προσθέτετε κλάσματα με τον ίδιο παρονομαστή. Εάν οι παρονομαστές είναι διαφορετικοί, διαβάστε τη δεύτερη μέθοδο.
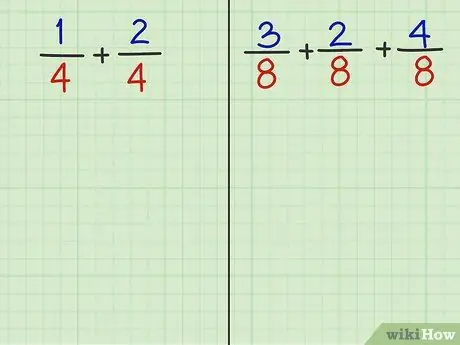
Βήμα 2. Απαντήστε στις ακόλουθες 2 ερωτήσεις
Διαβάζοντας το τελευταίο βήμα σε αυτήν τη μέθοδο, θα πρέπει να μπορείτε να προσθέσετε τα κλάσματα των δύο ακόλουθων ερωτήσεων.
- Πρόβλημα 1: 1/4 + 2/4
- Πρόβλημα 2: 3/8 + 2/8 + 4/8
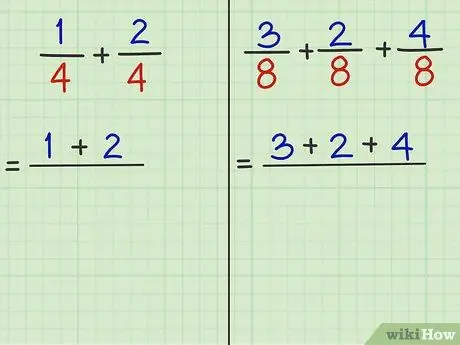
Βήμα 3. Συλλέξτε τους αριθμητές (τους αριθμούς πάνω από τη διαίρεση) και προσθέστε τους
Ο αριθμητής είναι ο αριθμός πάνω από το πηλίκο. Ανεξάρτητα από το πόσα κλάσματα θέλετε να προσθέσετε, μπορείτε να προσθέσετε τους αριθμητές αμέσως εάν οι παρονομαστές είναι ίδιοι.
- Πρόβλημα 1: 1/4 + 2/4 είναι το κλάσμα που πρέπει να προστεθεί. Τα "1" και "2" είναι αριθμητές. Άρα, 1 + 2 = 3.
- Πρόβλημα 2: 3/8 + 2/8 + 4/8 είναι το κλάσμα που πρέπει να προστεθεί. "3" και "2" και "4" είναι αριθμητές. Έτσι, 3 + 2 + 4 = 9.

Βήμα 4. Προσδιορίστε το νέο κλάσμα από το άθροισμα
Γράψτε τον αριθμητή που ελήφθη στο βήμα 2. Αυτός ο αριθμός είναι νέος αριθμητής Το Γράψτε τον παρονομαστή, ο οποίος είναι ο ίδιος αριθμός κάτω από τη διχοτόμο κάθε κλάσματος. Δεν χρειάζεται να κάνετε τους υπολογισμούς εάν οι παρονομαστές είναι οι ίδιοι. Αυτός ο αριθμός είναι νέος παρονομαστής και πάντα ισούται με τον παλιό παρονομαστή όταν προσθέτετε κλάσματα με τον ίδιο παρονομαστή.
- Πρόβλημα 1: 3 είναι ο νέος αριθμητής και 4 ο νέος παρονομαστής. Έτσι, η απάντηση στην ερώτηση 1 είναι 3/4. 1/4 + 2/4 = 3/4.
- Πρόβλημα 2: 9 είναι ο νέος αριθμητής και 8 ο νέος παρονομαστής. Έτσι, η απάντηση στην ερώτηση 2 είναι 9/8. 3/8 + 2/8 + 4/8 = 9/8.
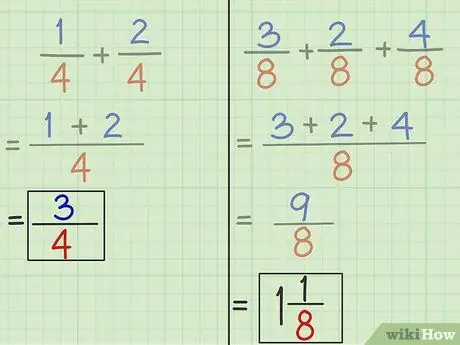
Βήμα 5. Απλοποιήστε τα κλάσματα εάν χρειάζεται
Μην ξεχάσετε να απλοποιήσετε το νέο κλάσμα για να κάνετε τη γραφή πιο απλή.
-
Αν ο αριθμητής μεγαλύτερος αντί για παρονομαστή όπως το αποτέλεσμα της προσθήκης του προβλήματος 2, αυτό σημαίνει ότι παίρνουμε 1 ολόκληρο μήνα μετά την απλοποίηση του κλάσματος. Διαιρέστε τον αριθμητή με τον παρονομαστή ή 9 διαιρούμενος με το 8. Το αποτέλεσμα είναι ένας ακέραιος 1 που απομένει 1. Γράψτε ακέραιοι μπροστά από το κλάσμα και το υπόλοιπο γίνεται ο αριθμητής ενός νέου κλάσματος με τον ίδιο παρονομαστή.
9/8 = 1 1/8.
Μέθοδος 2 από 2: Προσθήκη κλασμάτων με διαφορετικούς παρονομαστές

Βήμα 1. Ελέγξτε τον παρονομαστή (τον αριθμό κάτω από το πηλίκο) κάθε κλάσματος
Εάν οι παρονομαστές είναι διαφορετικοί, είστε προσθέστε κλάσματα με διαφορετικούς παρονομαστές Το Διαβάστε τα παρακάτω βήματα γιατί πρέπει να κάνετε τους παρονομαστές ίσους πριν προσθέσετε κλάσματα.
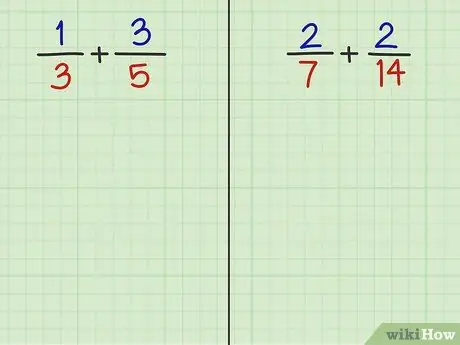
Βήμα 2. Λύστε τις ακόλουθες 2 ερωτήσεις
Διαβάζοντας το τελευταίο βήμα σε αυτήν τη μέθοδο, θα πρέπει να μπορείτε να προσθέσετε τα κλάσματα των δύο ακόλουθων ερωτήσεων.
- Πρόβλημα 3: 1/3 + 3/5
- Ερώτηση 4: 2/7 + 2/14

Βήμα 3. Αντιστοιχίστε τους παρονομαστές
Για να γίνει αυτό, πολλαπλασιάστε τους παρονομαστές των δύο παραπάνω κλασμάτων. Ένας εύκολος τρόπος εξίσωσης των παρονομαστών είναι ο πολλαπλασιασμός των παρονομαστών των δύο κλασμάτων. Εάν ένας από τους παρονομαστές είναι πολλαπλάσιος του άλλου, βρείτε το λιγότερο κοινό πολλαπλάσιο των δύο παρονομαστών.
-
Πρόβλημα 3:
3 x 5 = 15. Άρα, ο νέος παρονομαστής και των δύο κλασμάτων είναι 15.
-
Πρόβλημα 4:
Το 14 είναι πολλαπλάσιο του 7. Επομένως, χρειάζεται μόνο να πολλαπλασιάσουμε το 7 επί 2 για να πάρουμε 14. Έτσι, ο νέος παρονομαστής και των δύο κλασμάτων είναι το 14.

Βήμα 4. Πολλαπλασιάστε τον αριθμητή και τον παρονομαστή του πρώτου κλάσματος με τον παρονομαστή του δεύτερου κλάσματος
Αυτό το βήμα δεν αλλάζει την τιμή του κλάσματος, αλλά το κλάσμα φαίνεται να αλλάζει για να ταιριάζει με τον παρονομαστή. Η κλασματική τιμή παραμένει η ίδια.
-
Πρόβλημα 3:
1/3 x 5/5 = 5/15.
-
Πρόβλημα 4:
Για αυτό το πρόβλημα, πρέπει απλώς να πολλαπλασιάσουμε το πρώτο κλάσμα επί 2/2 για να έχουμε τους παρονομαστές ίσους.
2/7 x 2/2 = 4/14

Βήμα 5. Πολλαπλασιάστε τον αριθμητή και τον παρονομαστή του δεύτερου κλάσματος με τον παρονομαστή του πρώτου κλάσματος
Παρόμοια με τα παραπάνω βήματα, δεν αλλάζουμε την τιμή του κλάσματος, αλλά το κλάσμα φαίνεται να αλλάζει για να εξισωθεί ο παρονομαστής. Η κλασματική τιμή παραμένει η ίδια.
-
Πρόβλημα 3:
3/5 x 3/3 = 9/15.
-
Πρόβλημα 4:
Δεν χρειάζεται να πολλαπλασιάσουμε το δεύτερο κλάσμα γιατί οι παρονομαστές είναι ίδιοι.

Βήμα 6. Γράψτε τα δύο νέα κλάσματα με τη σειρά
Σε αυτό το σημείο, δεν έχουμε προσθέσει τα δύο κλάσματα μαζί, αν και μπορούμε. Στο παραπάνω βήμα, πολλαπλασιάσαμε κάθε κλάσμα επί 1. Τώρα, θέλουμε να βεβαιωθούμε ότι τα κλάσματα που θέλουμε να προσθέσουμε έχουν τον ίδιο παρονομαστή.
-
Πρόβλημα 3:
αντί για 1/3 + 3/5, το κλάσμα γίνεται 5/15 + 9/15
-
Πρόβλημα 4:
Αντί για 2/7 + 2/14, το κλάσμα γίνεται 4/14 + 2/14

Βήμα 7. Προσθέστε τους αριθμητές των δύο κλασμάτων μαζί
Ο αριθμητής είναι ο αριθμός πάνω από το πηλίκο.
-
Πρόβλημα 3:
5 + 9 = 14. 14 είναι ο νέος αριθμητής.
-
Πρόβλημα 4:
4 + 2 = 6. 6 είναι ο νέος αριθμητής.

Βήμα 8. Γράψτε τον κοινό παρονομαστή (στο βήμα 2) κάτω από τον νέο αριθμητή ή χρησιμοποιήστε τον παρονομαστή του κλάσματος πολλαπλασιασμένο με 1 για να εξισώσετε τον παρονομαστή
-
Πρόβλημα 3:
15 είναι ο νέος παρονομαστής.
-
Πρόβλημα 4:
14 είναι ο νέος παρονομαστής.

Βήμα 9. Γράψτε έναν νέο αριθμητή και έναν νέο παρονομαστή
-
Πρόβλημα 3:
14/15 είναι η απάντηση 1/3 + 3/5 =;
-
Πρόβλημα 4:
6/14 είναι η απάντηση 2/7 + 2/14 =;

Βήμα 10. Απλοποιήστε και μειώστε τα κλάσματα
Για να απλοποιήσουμε τα κλάσματα, διαιρούμε τον αριθμητή και τον παρονομαστή με τον μεγαλύτερο κοινό συντελεστή των δύο αριθμών.
-
Πρόβλημα 3:
14/15 δεν μπορεί να απλοποιηθεί.
-
Πρόβλημα 4:
Το 6/14 μπορεί να μειωθεί σε 3/7 αφού διαιρέσετε τον αριθμητή και τον παρονομαστή με το 2 ως τον μεγαλύτερο κοινό συντελεστή των 6 και 14.
Συμβουλές
- Πριν προσθέσετε κλάσματα, βεβαιωθείτε ότι οι παρονομαστές είναι οι ίδιοι.
- Μην αθροίζετε τους παρονομαστές. Εάν οι παρονομαστές είναι ίδιοι, χρησιμοποιήστε τον αριθμό ως παρονομαστή αφού προστεθούν τα κλάσματα.
- Εάν θέλετε να προσθέσετε κλάσματα με αριθμούς που αποτελούνται από ακέραιους αριθμούς και κλάσματα, μετατρέψτε αυτούς τους αριθμούς σε κλάσματα και προσθέστε τους σύμφωνα με τις παραπάνω οδηγίες.






