- Συγγραφέας Jason Gerald [email protected].
- Public 2024-01-19 22:12.
- Τελευταία τροποποίηση 2025-01-23 12:15.
Εάν γνωρίζετε πώς να υπολογίζετε τις πληρωμές δανείων, μπορείτε να προγραμματίσετε τον δικό σας προϋπολογισμό, ώστε να μην εκπλαγείτε αργότερα. Συνιστάται να χρησιμοποιείτε μια ηλεκτρονική αριθμομηχανή δανείου επειδή ο υπολογισμός χρησιμοποιώντας μια κανονική αριθμομηχανή που χρησιμοποιεί μεγάλους τύπους σας διευκολύνει να κάνετε λάθη.
Βήμα
Μέθοδος 1 από 3: Χρήση ηλεκτρονικής αριθμομηχανής

Βήμα 1. Ανοίξτε μια ηλεκτρονική αριθμομηχανή δανείου
Μπορείτε να πατήσετε την αριθμομηχανή στην ενότητα δείγματα στο επάνω μέρος της σελίδας και, στη συνέχεια, να την ανοίξετε με το Google Drive ή να την κατεβάσετε, ώστε να μπορείτε να την ανοίξετε με Excel ή άλλο πρόγραμμα. Επιπλέον, ανοίξτε έναν από τους παρακάτω συνδέσμους:
- Το Bankrate.com και το MLCalc είναι και οι δύο απλοί υπολογιστές που σας δείχνουν επίσης έναν ολόκληρο πίνακα του χρονοδιαγράμματος πληρωμών σας, συμπεριλαμβανομένου του υπολειπόμενου χρέους σας.
- Το CalculatorSoup είναι ιδιαίτερα χρήσιμο για ασυνήθιστες πληρωμές ή χρήση αυξημένων διαστημάτων. Για παράδειγμα, τα στεγαστικά δάνεια στον Καναδά προστίθενται συνήθως κάθε έξι μήνες ή δύο φορές το χρόνο. (Ο παραπάνω υπολογιστής υποθέτει ότι οι τόκοι προστίθενται μηνιαίως και οι πληρωμές γίνονται μηνιαίως.)
- Μπορείτε να δημιουργήσετε τη δική σας αριθμομηχανή στο Excel, παρόμοια με το παράδειγμα από το wikiHow παραπάνω.
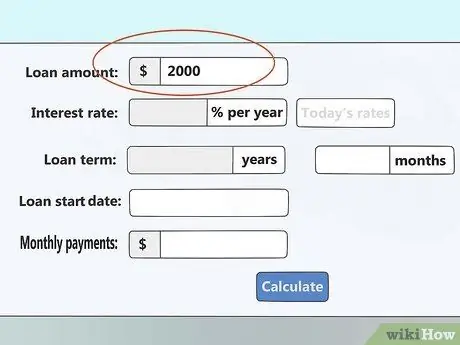
Βήμα 2. Εισαγάγετε το ποσό του δανείου
Αυτό είναι το συνολικό ποσό των χρημάτων που έχετε δανειστεί. Εάν θέλετε να υπολογίσετε ένα μερικώς πληρωμένο χρέος, εισαγάγετε το υπόλοιπο χρέος που εξακολουθείτε να χρωστάτε.
Αυτή η στήλη μπορεί να έχει τίτλο "βασικό ποσό"
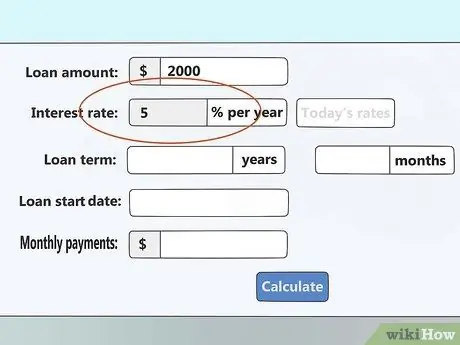
Βήμα 3. Εισαγάγετε το επιτόκιο
Αυτό είναι το τρέχον επιτόκιο του δανείου σας και είναι σε ποσοστό. Για παράδειγμα, εάν πρέπει να πληρώσετε επιτόκιο 6%, πληκτρολογήστε έναν αριθμό
Βήμα 6
Το διάστημα αύξησης δεν έχει σημασία εδώ. Το επιτόκιο που καθορίζεται πρέπει να είναι το ετήσιο ποσό τόκου, ακόμη και αν ο τόκος αυτός υπολογίζεται συχνότερα

Βήμα 4. Εισαγάγετε τη διάρκεια του δανείου
Αυτός είναι ο χρόνος που σκοπεύετε να εξοφλήσετε το χρέος σας. Χρησιμοποιήστε το χρονικό διάστημα που καθορίζεται στην πολιτική δανείου για να υπολογίσετε την ελάχιστη μηνιαία πληρωμή που πρέπει να πραγματοποιηθεί. Χρησιμοποιήστε μικρότερο χρονικό διάστημα για να υπολογίσετε υψηλότερες πληρωμές, ώστε να μπορείτε να εξοφλήσετε γρήγορα τα χρέη σας.
- Ταχύτερη εξόφληση χρεών σημαίνει επίσης λιγότερα χρήματα που δαπανώνται.
- Ανατρέξτε στον παρακάτω πίνακα σε αυτήν τη στήλη για να διαπιστώσετε εάν αυτός ο υπολογιστής χρησιμοποιεί μηνιαίο ή ετήσιο σύστημα.

Βήμα 5. Εισαγάγετε την ημερομηνία έναρξης
Αυτό χρησιμοποιείται για τον υπολογισμό σε ποια ημερομηνία θα εξοφλήσετε το δάνειο.
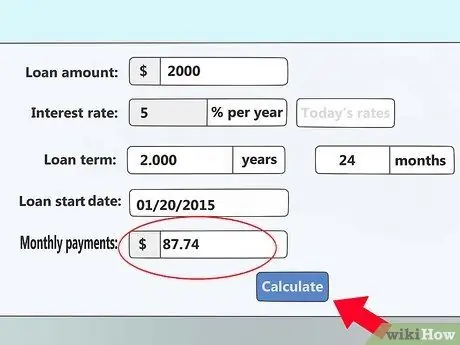
Βήμα 6. Πατήστε υπολογισμός (υπολογισμός
) Ορισμένοι υπολογιστές θα ενημερώσουν αυτόματα το πεδίο "Μηνιαία πληρωμή" αφού εισαγάγετε τις πληροφορίες. Ωστόσο, ορισμένοι πρέπει να περιμένουν να πατήσετε το κουμπί "υπολογισμός", για να εμφανιστεί ένα γράφημα του χρονοδιαγράμματος πληρωμής σας.
- Το "Κύριο Δάνειο" είναι το υπόλοιπο του αρχικού χρέους, ενώ το "Επιτόκιο" είναι το επιπλέον κόστος του δανείου.
- Αυτοί οι υπολογιστές θα σας δείξουν πληροφορίες σχετικά με το χρονοδιάγραμμα αποπληρωμής του δανείου σας σε απόσβεση (πίστωση που εξοφλείται σε κανονικές δόσεις), πράγμα που σημαίνει ότι θα πληρώνετε το ίδιο ποσό κάθε μήνα.
- Εάν πληρώσετε λιγότερο από το ποσό που εμφανίζεται, θα πρέπει να κάνετε μια ενιαία, πολύ μεγάλη πληρωμή στο τέλος της διάρκειας του δανείου και πρέπει να πληρώσετε μεγαλύτερο ποσό.
Μέθοδος 2 από 3: Υπολογισμός των πληρωμών δανείου με μη αυτόματο τρόπο
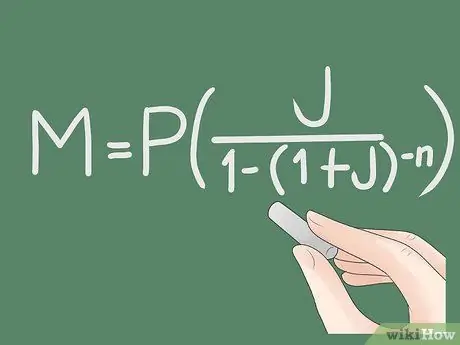
Βήμα 1. Γράψτε τον τύπο που χρησιμοποιείται
Ο τύπος που χρησιμοποιείται για τον υπολογισμό των πληρωμών δανείων είναι M = P * (J / (1 - (1 + J)-Ν)) Το Ακολουθήστε αυτά τα βήματα για να σας καθοδηγήσουμε χρησιμοποιώντας αυτόν τον τύπο ή ακολουθήστε μια σύντομη εξήγηση για κάθε μεταβλητή:
- M = ποσό πληρωμής
- P = κύριο κεφάλαιο, δηλαδή το ποσό των χρημάτων που δανείζεστε
- J = πραγματικό επιτόκιο. Λάβετε υπόψη ότι αυτό γενικά δεν είναι ετήσιο επιτόκιο, δείτε την εξήγηση παρακάτω.
- N = πόσες φορές να πληρώσετε

Βήμα 2. Να είστε προσεκτικοί στη στρογγυλοποίηση των αποτελεσμάτων
Στην ιδανική περίπτωση, χρησιμοποιήστε μια αριθμομηχανή γραφικών ή ένα λογισμικό αριθμομηχανής για να υπολογίσετε ολόκληρο τον τύπο σε μία γραμμή. Εάν χρησιμοποιείτε αριθμομηχανή που μπορεί να εκτελέσει μόνο βήμα προς βήμα υπολογισμούς ή αν θέλετε να ακολουθήσετε τα παρακάτω λεπτομερή βήματα, στρογγυλοποιήστε σε τουλάχιστον τέσσερα σημαντικά στοιχεία πριν προχωρήσετε στο επόμενο βήμα. Η στρογγυλοποίηση σε μικρότερο δεκαδικό μπορεί να οδηγήσει σε σημαντικά σφάλματα στρογγυλοποίησης στην τελική απάντησή σας.
- Ακόμη και οι απλοί αριθμομηχανές έχουν συνήθως ένα κουμπί "Ans". Αυτό το κουμπί χρησιμοποιείται για την εισαγωγή της προηγούμενης απάντησης στον επόμενο υπολογισμό, το αποτέλεσμα του οποίου θα είναι πιο ακριβές από τον παρακάτω υπολογισμό.
- Τα παρακάτω παραδείγματα στρογγυλοποιούνται μετά από κάθε βήμα, αλλά το τελευταίο βήμα περιλαμβάνει την απάντηση που θα λάβετε εάν ολοκληρώσετε τον υπολογισμό σε μία γραμμή, ώστε να μπορείτε να ελέγξετε ξανά την εργασία σας.
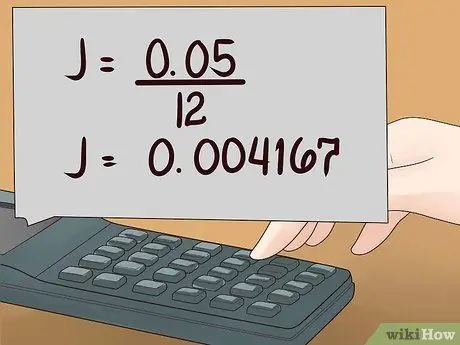
Βήμα 3. Υπολογίστε το πραγματικό σας επιτόκιο J
Οι πολιτικές δανείων συνήθως αναφέρουν ένα "ετήσιο επιτόκιο", αλλά δεν μπορείτε να εξοφλήσετε το δάνειό σας σε ετήσιες δόσεις. Διαιρέστε το ετήσιο επιτόκιο με 100 για να λάβετε ένα δεκαδικό, στη συνέχεια διαιρέστε με τον αριθμό των φορών που πληρώνετε το δάνειό σας κάθε χρόνο για να λάβετε το πραγματικό επιτόκιο.
- Για παράδειγμα, εάν το ετήσιο επιτόκιο σας είναι 5%και πληρώνετε σε μηνιαίες δόσεις (12 φορές το χρόνο), υπολογίστε 5/100 για να λάβετε 0,05 και στη συνέχεια υπολογίστε J = 0,05 / 12 = 0, 004167.
- Σε ασυνήθιστες περιπτώσεις, τα επιτόκια υπολογίζονται σε διαφορετικά διαστήματα από το χρονοδιάγραμμα πληρωμών. Το πιο αξιοσημείωτο είναι ότι τα στεγαστικά δάνεια στον Καναδά υπολογίζονται συνήθως δύο φορές το χρόνο, αν και οι δανειολήπτες πραγματοποιούν πληρωμές 12 φορές ετησίως. Σε αυτήν την περίπτωση, πρέπει να διαιρέσετε το ετήσιο επιτόκιο με δύο.

Βήμα 4. Δώστε προσοχή στο συνολικό αριθμό πληρωμών Ν
Η δανειακή σας πολιτική μπορεί να καθορίζει ήδη αυτόν τον αριθμό ή μπορεί να χρειαστεί να τον υπολογίσετε μόνοι σας. Για παράδειγμα, εάν η διάρκεια του δανείου είναι 5 έτη και θα πληρώνετε σε μηνιαίες δόσεις 12 φορές το χρόνο, τότε ο συνολικός αριθμός των πληρωμών σας είναι N = 5 * 12 = 60.
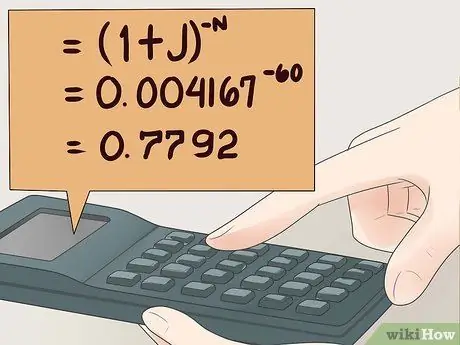
Βήμα 5. Υπολογίστε (1+J)-Ν.
Προσθέστε πρώτα 1+J και, στη συνέχεια, αυξήστε την απάντηση στη δύναμη του "-N". Βεβαιωθείτε ότι έχετε βάλει αρνητικό πρόσημο μπροστά από το Ν. Εάν η αριθμομηχανή σας δεν λειτουργεί με αρνητικούς εκθέτες, μπορείτε να γράψετε 1/((1+J)Ν).
Σε αυτό το παράδειγμα, (1+J)-Ν = (1.004167)-60 = 0, 7792

Βήμα 6. Υπολογίστε το J/(1- (η απάντησή σας))
Με μια απλή αριθμομηχανή, υπολογίστε πρώτα το 1 - τον αριθμό που υπολογίσατε στο προηγούμενο βήμα. Στη συνέχεια, υπολογίστε το J διαιρούμενο με το αποτέλεσμα, χρησιμοποιώντας το πραγματικό επιτόκιο για τον υπολογισμό του "J" παραπάνω.
Σε αυτό το παράδειγμα, J/(1- (η απάντησή σας)) = 0, 004167/(1-0,7792) = 0, 01887

Βήμα 7. Βρείτε το ποσό της μηνιαίας πληρωμής σας
Για να το υπολογίσετε, πολλαπλασιάστε το τελικό σας αποτέλεσμα με το ποσό του δανείου P. Το αποτέλεσμα είναι το χρηματικό ποσό που πρέπει να πληρώνετε κάθε μήνα για να εξοφλήσετε το δάνειό σας εγκαίρως.
- Για παράδειγμα, αν δανειστήκατε $ 30.000, θα πολλαπλασιάσετε την τελευταία σας απάντηση με 30.000. Συνεχίζοντας το παραπάνω παράδειγμα, 0.01887 * 30.000 = 566, 1 δολάρια κάθε μήνα, ή 566 δολάρια και 10 σεντ.
- Αυτό ισχύει για όλα τα νομίσματα, όχι μόνο για τα δολάρια.
- Εάν υπολογίσετε όλα αυτά τα παραδείγματα σε μια γραμμή χρησιμοποιώντας έναν φανταχτερό υπολογιστή, θα λάβετε μια πιο ακριβή κύρια απάντηση πληρωμής, το αποτέλεσμα είναι πολύ κοντά στα $ 566, 137 ή περίπου $ 566 και 14 σεντ κάθε μήνα. Αν πληρώναμε ακόμη και 566 δολάρια και 10 σεντ κάθε μήνα όπως υπολογίζαμε με τον λιγότερο ακριβή αριθμομηχανή παραπάνω, θα είχαμε κάνει μια μικρή διαφορά στο τέλος της διάρκειας του δανείου και ίσως χρειαζόταν να πληρώσουμε μερικά δολάρια παραπάνω (λιγότερο από 5 σε αυτό υπόθεση.)
Μέθοδος 3 από 3: Κατανόηση του τρόπου λειτουργίας των δανείων

Βήμα 1. Κατανοήστε τη διαφορά μεταξύ δανείου σταθερού επιτοκίου και δανείου με ρυθμιζόμενο επιτόκιο
Όλα τα δάνεια χρησιμοποιούν μία από αυτές τις δύο κατηγορίες. Βεβαιωθείτε ότι γνωρίζετε τι τύπος εφαρμόζεται στο δάνειό σας:
- Δάνεια με σταθερό ενδιαφέρον έχει σταθερό επιτόκιο. Η μηνιαία πληρωμή σας δεν θα αλλάξει ποτέ αρκεί να πληρώσετε εγκαίρως.
- Δάνεια με προσαρμοσμένα λουλούδια θα προσαρμόζεται περιοδικά στο τρέχον τυπικό επιτόκιο, οπότε μπορεί να καταλήξετε σε περισσότερο ή λιγότερο χρέος εάν αλλάξουν τα επιτόκια. Το επιτόκιο επανυπολογίζεται μόνο κατά τη διάρκεια της "περιόδου προσαρμογής" που καθορίζεται στην δανειακή σας πολιτική. Εάν γνωρίζετε ότι το τρέχον επιτόκιο είναι μόνο λίγους μήνες πριν από την επόμενη περίοδο προσαρμογής, μπορείτε να προγραμματίσετε εκ των προτέρων.

Βήμα 2. Κατανοήστε την απόσβεση
Η απόσβεση αναφέρεται στο ποσοστό με το οποίο μειώνεται το αρχικό ποσό που δανειστήκατε (το κύριο δάνειο). Σε γενικές γραμμές, υπάρχουν δύο τύποι προγραμμάτων αποπληρωμής δανείου:
- Πληρωμή δανείου με πλήρη απόσβεση υπολογίζεται έτσι ώστε να μπορείτε να πληρώνετε ένα σταθερό ποσό κάθε μήνα για ολόκληρη την περίοδο αποπληρωμής, εξοφλώντας το κεφάλαιο και τα επιτόκια με κάθε πληρωμή. Οι αριθμομηχανές και οι παραπάνω τύποι υποθέτουν ότι θέλετε ένα πρόγραμμα όπως αυτό.
- Σχέδιο αποπληρωμής δανείου με πληρώστε μόνο τους τόκους σας δίνει χαμηλότερη αρχική πληρωμή κατά την περίοδο "μόνο για τόκους", επειδή εξοφλείτε μόνο τους τόκους, όχι το αρχικό δάνειο "κεφαλαίου". Αφού τελειώσει η περίοδος τόκων, οι μηνιαίες πληρωμές σας θα είναι τεράστιες, γιατί θα αρχίσετε να εξοφλείτε και το κεφάλαιο και τους τόκους. Αυτό θα σας κοστίσει περισσότερα χρήματα μακροπρόθεσμα.

Βήμα 3. Πληρώστε περισσότερα χρήματα εκ των προτέρων για να εξοικονομήσετε περισσότερα χρήματα μακροπρόθεσμα
Η πραγματοποίηση πρόσθετων πληρωμών θα μειώσει το χρηματικό ποσό που πρέπει να δαπανήσετε μακροπρόθεσμα, διότι όσο μικρότερο είναι το ποσό του δανείου στο οποίο βασίζεται ο υπολογισμός των τόκων. Όσο πιο γρήγορα το κάνετε αυτό, τόσο περισσότερα χρήματα μπορείτε να εξοικονομήσετε.






