- Συγγραφέας Jason Gerald gerald@how-what-advice.com.
- Public 2024-01-19 22:12.
- Τελευταία τροποποίηση 2025-01-23 12:15.
Η αφαίρεση είναι απλά η αφαίρεση ενός αριθμού από τον άλλο. Είναι εύκολο να αφαιρέσετε έναν ακέραιο αριθμό από έναν άλλο, αλλά η αφαίρεση μπορεί να είναι δύσκολη εάν αφαιρείτε κλάσματα ή δεκαδικά ψηφία. Μόλις κατανοήσετε την αφαίρεση, θα μπορείτε να χρησιμοποιήσετε πιο σύνθετες μαθηματικές έννοιες και θα μπορείτε να προσθέσετε, να πολλαπλασιάσετε και να διαιρέσετε αριθμούς πιο εύκολα.
Βήμα
Μέθοδος 1 από 6: Αφαίρεση μεγάλων αριθμών με δανεισμό

Βήμα 1. Γράψτε έναν μεγάλο αριθμό
Για παράδειγμα, θέλετε να λύσετε 32 - 17. Γράψτε πρώτα 32.

Βήμα 2. Γράψτε τον μικρότερο αριθμό ακριβώς από κάτω
Βεβαιωθείτε ότι τοποθετείτε τις τιμές των δεκάδων και των μονάδων στις σωστές στήλες, έτσι ώστε το 3 από το 32 να βρίσκεται ακριβώς πάνω από το 1 του 17 και το 2 από το 32 να βρίσκεται ακριβώς πάνω από το 7 του 17.
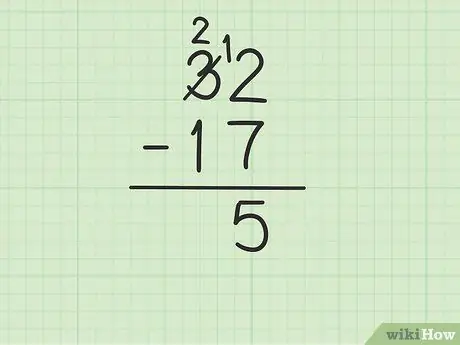
Βήμα 3. Αφαιρέστε τον επάνω αριθμό στη στήλη μονάδες από τον αριθμό στο κάτω μέρος
Ωστόσο, αυτό μπορεί να γίνει περίπλοκο εάν ο κάτω αριθμός είναι μεγαλύτερος από τον επάνω αριθμό. Σε αυτήν την περίπτωση, το 7 είναι μεγαλύτερο από το 2. Δείτε τι πρέπει να κάνετε:
- Πρέπει να δανειστείτε από τον αριθμό 3 των 32 (γνωστός και ως ομαδοποίηση), για να μετατρέψετε το 2 σε 12.
- Σταυρώστε τον αριθμό 3 από τους 32 και αντικαταστήστε τον με τον αριθμό 2, ενώ ο αριθμός 2 γίνεται 12.
- Τώρα μπορείτε να αφαιρέσετε 12 - 7, που ισούται με 5. Γράψτε 5 κάτω από τους δύο αριθμούς που αφαιρείτε, ώστε να βρίσκονται στη στήλη μονάδων της νέας σειράς.
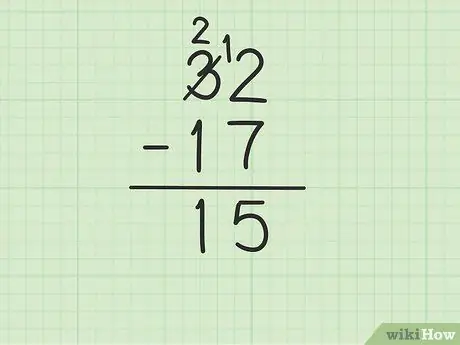
Βήμα 4. Αφαιρέστε τον επάνω αριθμό στη στήλη δεκάδες από τον κάτω αριθμό
Θυμηθείτε ότι το 3 έγινε 2. Τώρα αφαιρέστε το 1 από το 17 από τα 2 παραπάνω για να πάρετε (2-1) 1. Γράψτε 1 παρακάτω, στη στήλη των δεκάδων, στα αριστερά του 5 στη στήλη μονάδων. Γράφετε 15. Δηλαδή 32 - 17 = 15.
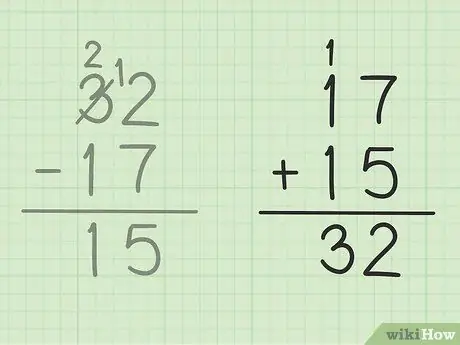
Βήμα 5. Ελέγξτε την εργασία σας
Εάν θέλετε να βεβαιωθείτε ότι έχετε αφαιρέσει δύο αριθμούς σωστά, τότε το μόνο που έχετε να κάνετε είναι να προσθέσετε την απάντησή σας με τον μικρότερο αριθμό για να δημιουργήσετε έναν μεγάλο αριθμό. Σε αυτό το πρόβλημα, πρέπει να προσθέσετε την απάντησή σας, 15 στον μικρότερο αριθμό αφαίρεσης, 17. 15 + 17 = 32, έτσι ώστε η απάντησή σας να είναι σωστή. Ασφαλής!
Μέθοδος 2 από 6: Αφαίρεση μικρών ολόκληρων αριθμών
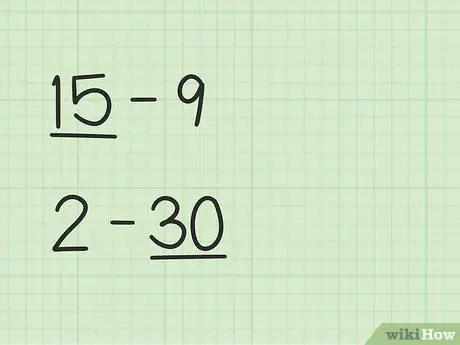
Βήμα 1. Βρείτε τον μεγαλύτερο αριθμό
Προβλήματα όπως 15 -9 θα έχουν διαφορετικό τρόπο από 2 -30.
- Στις ερωτήσεις 15 - 9, ο πρώτος αριθμός, 15, είναι μεγαλύτερος από τον δεύτερο αριθμό, 9.
- Στις ερωτήσεις 2 - 30, ο δεύτερος αριθμός, 30, είναι μεγαλύτερος από τον πρώτο αριθμό, 2.
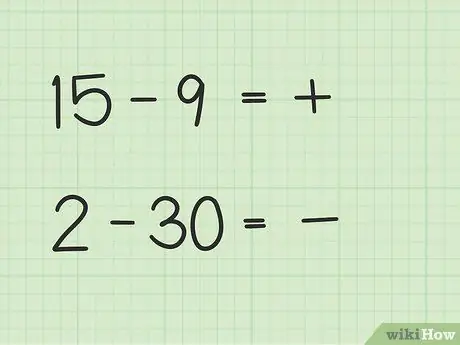
Βήμα 2. Αποφασίστε αν η απάντησή σας θα είναι θετική ή αρνητική
Εάν ο πρώτος αριθμός είναι μεγαλύτερος, η απάντηση είναι θετική. Εάν ο δεύτερος αριθμός είναι μεγαλύτερος, η απάντηση είναι αρνητική.
- Στην πρώτη ερώτηση, 15 - 9, η απάντησή σας είναι θετική επειδή ο πρώτος αριθμός είναι μεγαλύτερος από τον δεύτερο αριθμό.
- Στη δεύτερη ερώτηση, 2 - 30, η απάντησή σας είναι αρνητική επειδή ο δεύτερος αριθμός είναι μεγαλύτερος από τον πρώτο αριθμό.
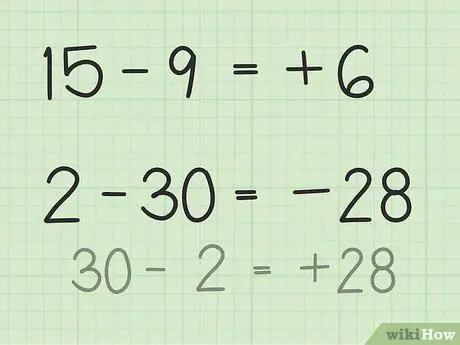
Βήμα 3. Βρείτε τη διαφορά μεταξύ δύο αριθμών
Για να αφαιρέσετε δύο αριθμούς, πρέπει να φανταστείτε τη διαφορά μεταξύ των δύο αριθμών και να υπολογίσετε τους αριθμούς μεταξύ τους.
- Για τις ερωτήσεις 15 - 9, φανταστείτε μια στοίβα 15 μάρκες πόκερ. Πετάξτε 9 μάρκες και μόνο 6. Έτσι, 15 - 9 = 6. Μπορείτε επίσης να φανταστείτε μια αριθμητική γραμμή. Σκεφτείτε τους αριθμούς από το 1 έως το 15, στη συνέχεια απορρίψτε ή επιστρέψτε 9 μονάδες για να πάρετε 6.
- Για τις ερωτήσεις 2 - 30, ο ευκολότερος τρόπος για να το λύσετε αυτό είναι να αντιστρέψετε τον αριθμό και να κάνετε το αποτέλεσμα αρνητικό μετά την αφαίρεση. Έτσι, 30 - 2 = 28 άρα 28 και 30 έχουν διαφορά 2. Τώρα, κάντε το αποτέλεσμα αρνητικό επειδή έχετε ήδη καθορίσει ότι η απάντηση είναι αρνητική επειδή ο δεύτερος αριθμός είναι μεγαλύτερος από τον πρώτο αριθμό. Έτσι, 2 -30 = -28.
Μέθοδος 3 από 6: Αφαίρεση δεκαδικών
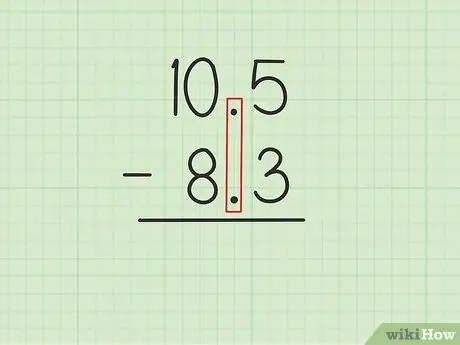
Βήμα 1. Γράψτε τον μεγαλύτερο αριθμό πάνω από τον μικρότερο αριθμό με τα δεκαδικά ψηφία ευθυγραμμισμένα
Ας υποθέσουμε ότι θέλετε να λύσετε τα ακόλουθα προβλήματα: 10, 5 - 8, 3. Γράψτε 10, 5 επί 8, 3 έτσι ώστε τα δεκαδικά ψηφία των δύο αριθμών να είναι παράλληλα., 5 από 10, 5 πρέπει να είναι ακριβώς πάνω, 3 από 8, 3 και 0 από 10, 5 πρέπει να είναι πάνω από 8 από 8, 3.
Εάν αντιμετωπίζετε πρόβλημα επειδή οι δύο αριθμοί δεν έχουν τον ίδιο αριθμό μετά την υποδιαστολή, γράψτε 0 στο κενό μέχρι το άθροισμα των αριθμών να είναι το ίδιο. Για παράδειγμα, το πρόβλημα είναι 5, 32 - 4, 2, μπορείτε να το γράψετε ως 5, 32 - 4, 2 0 Το Αυτό δεν θα αλλάξει την τιμή του δεύτερου αριθμού, αλλά θα κάνει την αφαίρεση των δύο αριθμών ευκολότερη.

Βήμα 2. Αφαιρέστε τον επάνω αριθμό στη στήλη δεκάδες από τον παρακάτω αριθμό
Σε αυτή την περίπτωση, πρέπει να αφαιρέσετε το 3 από το 5. 5 - 3 = 2, οπότε πρέπει να γράψετε 2 κάτω από 3 από 8, 3.
Βεβαιωθείτε ότι έχετε βάλει ένα δεκαδικό σημείο στην απάντηση, έτσι ώστε να είναι γραμμένο, 2

Βήμα 3. Αφαιρέστε τον αριθμό πάνω από τη στήλη μονάδων από τον αριθμό κάτω από αυτήν
Πρέπει να αφαιρέσετε το 8 από το 0. Δανείστε 1 από το τμήμα των δεκάδων για να αλλάξετε 0 σε 10 και αφαιρέστε το 10 - 8 για να πάρετε 2. Μπορείτε επίσης να μετρήσετε 10 - 8 χωρίς να δανειστείτε επειδή δεν υπάρχουν αριθμοί στη δεύτερη δεκάδα. Γράψτε την απάντηση κάτω από το 8, αριστερά της υποδιαστολής.

Βήμα 4. Γράψτε το τελικό σας αποτέλεσμα
Το τελικό σας αποτέλεσμα είναι 2, 2.

Βήμα 5. Ελέγξτε την εργασία σας
Αν θέλετε να βεβαιωθείτε ότι η δεκαδική σας αφαίρεση είναι σωστή, το μόνο που έχετε να κάνετε είναι να προσθέσετε την απάντησή σας με τον μικρότερο αριθμό για να κάνετε τον μεγαλύτερο αριθμό. 2, 2 + 8, 3 = 10, 5, οπότε τελειώσατε.
Μέθοδος 4 από 6: Αφαίρεση κλασμάτων

Βήμα 1. Ευθυγραμμίστε τον παρονομαστή και τον αριθμητή του κλάσματος
Ας υποθέσουμε ότι θέλετε να λύσετε προβλήματα 13/10 - 3/5. Γράψτε το πρόβλημα έτσι ώστε οι δύο αριθμητές, 13 και 3 και οι δύο παρονομαστές, 10 και 5 να βρίσκονται ο ένας απέναντι από τον άλλο. Αυτοί οι δύο αριθμοί χωρίζονται με ένα σύμβολο αφαίρεσης. Αυτό θα σας βοηθήσει να απεικονίσετε το πρόβλημα και να το λύσετε πιο εύκολα.

Βήμα 2. Βρείτε τον λιγότερο κοινό παρονομαστή
Ο λιγότερο κοινός παρονομαστής είναι ο μικρότερος αριθμός που μπορεί να διαιρεθεί με δύο αριθμούς. Σε αυτό το παράδειγμα, πρέπει να βρείτε τον μικρότερο κοινό παρονομαστή που διαιρείται με 10 και 5. Θα διαπιστώσετε ότι το 10 είναι ο μικρότερος κοινός παρονομαστής και για τους δύο αριθμούς επειδή το 10 διαιρείται με το 10 και το 5.
Σημειώστε ότι ο ελάχιστος κοινός παρονομαστής δύο αριθμών δεν είναι πάντα ένας από αυτούς. Για παράδειγμα, ο μικρότερος κοινός παρονομαστής για το 3 και το 2 είναι 6 επειδή το 6 είναι ο μικρότερος αριθμός που μπορεί να διαιρεθεί με δύο αριθμούς
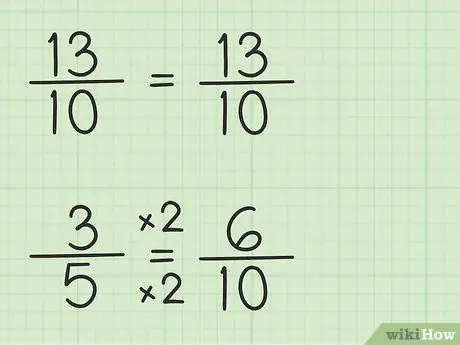
Βήμα 3. Γράψτε τα κλάσματα χρησιμοποιώντας τον ίδιο παρονομαστή
Το κλάσμα 13/10 μπορεί να γραφτεί με τον ίδιο τρόπο επειδή ο παρονομαστής είναι 10, ο μικρότερος κοινός παρονομαστής, ο οποίος είναι 10, επί το 1. Ωστόσο, το κλάσμα 3/5 πρέπει να ξαναγραφεί επειδή ο παρονομαστής είναι 5, ο μικρότερος κοινός παρονομαστής, το οποίο είναι 10, φορές 2. Άρα το κλάσμα 3/5 πρέπει να πολλαπλασιαστεί με 2/2 για να γίνει ο παρονομαστής 10, άρα 3/5 x 2/2 = 6/10. Βρήκατε το αντίστοιχο κλάσμα. Το 3/5 ισοδυναμεί με 6/10 αν και το 6/10 σας επιτρέπει να αφαιρέσετε τον πρώτο αριθμό, 13/10.
Γράψτε μια νέα ερώτηση όπως αυτή: 13/10 - 6/10
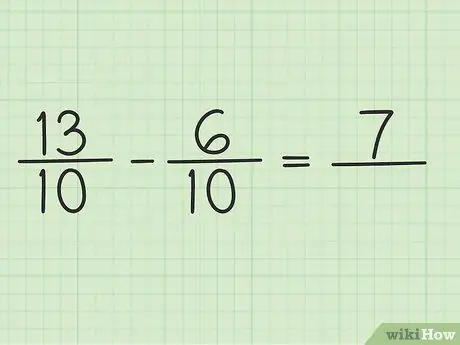
Βήμα 4. Αφαιρέστε τον αριθμητή σε δύο αριθμούς
Απλώς αφαιρέστε 13 - 6 οπότε το αποτέλεσμα είναι 7. Δεν μπορείτε να αλλάξετε τον παρονομαστή του κλάσματος.
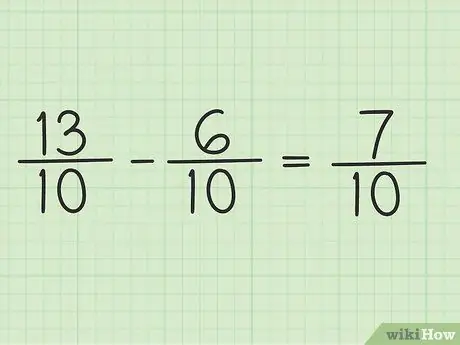
Βήμα 5. Γράψτε τον νέο αριθμητή στον ίδιο παρονομαστή για να λάβετε το τελικό αποτέλεσμα
Ο νέος αριθμητής είναι 7. Και τα δύο κλάσματα έχουν παρονομαστή 10. Το τελικό σας αποτέλεσμα είναι 7/10.
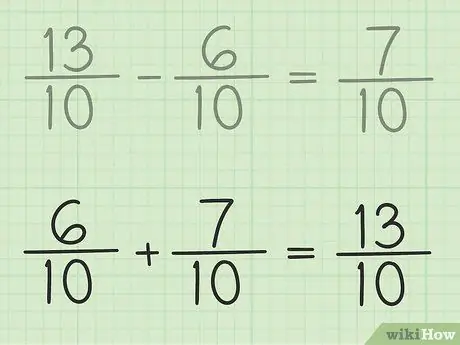
Βήμα 6. Ελέγξτε την εργασία σας
Αν θέλετε να βεβαιωθείτε ότι αφαιρείτε σωστά το κλάσμα, απλώς προσθέστε την απάντησή σας και το μικρότερο κλάσμα έτσι ώστε το αποτέλεσμα να είναι μεγαλύτερο κλάσμα. 7/10 + 6/10 = 13/10. Εχει τελειώσει.
Μέθοδος 5 από 6: Αφαίρεση κλασμάτων από ολόκληρους αριθμούς

Βήμα 1. Γράψτε το πρόβλημα
Για παράδειγμα, ας υποθέσουμε ότι θέλετε να λύσετε το ακόλουθο πρόβλημα: 5 -. Σημειώστε το.
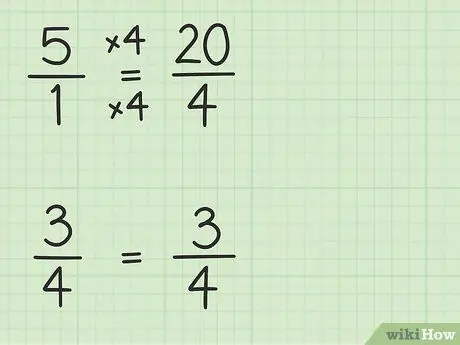
Βήμα 2. Μετατρέψτε ακέραιους αριθμούς σε κλάσματα που έχουν τον ίδιο παρονομαστή με άλλα κλάσματα
Θα μετατρέψετε το 5 σε κλάσμα με παρονομαστή το 4 για να μπορείτε να αφαιρέσετε δύο αριθμούς. Πρέπει λοιπόν να σκεφτείτε το 5 ως κλάσμα του 5/1. Στη συνέχεια, μπορείτε να πολλαπλασιάσετε τον αριθμητή και τον παρονομαστή του νέου κλάσματος με 4 για να κάνετε τους παρονομαστές των δύο αριθμών ίδιους. Άρα 5/1 x 4/4 = 20/4. Αυτό το κλάσμα είναι ίσο με 5, αλλά σας επιτρέπει να αφαιρέσετε δύο αριθμούς.
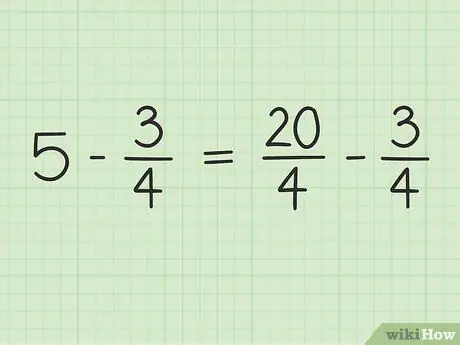
Βήμα 3. Ξαναγράψτε το πρόβλημα
Το νέο πρόβλημα μπορεί να γραφτεί ως εξής: 20/4 - 3/4.
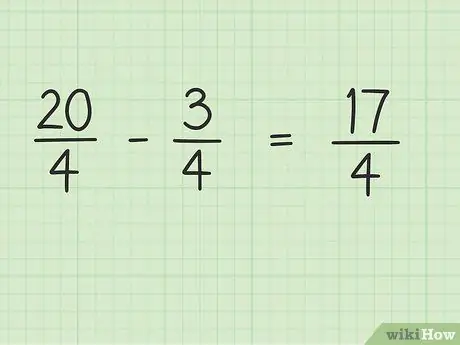
Βήμα 4. Αφαιρέστε τον αριθμητή του κλάσματος, ενώ ο παρονομαστής παραμένει ο ίδιος
Τώρα, απλά αφαιρέστε 20 επί 3 για να πάρετε το τελικό αποτέλεσμα. 20 - 3 = 17, άρα το 17 είναι ο νέος αριθμητής. Μπορείτε να αφήσετε τον παρονομαστή το ίδιο.
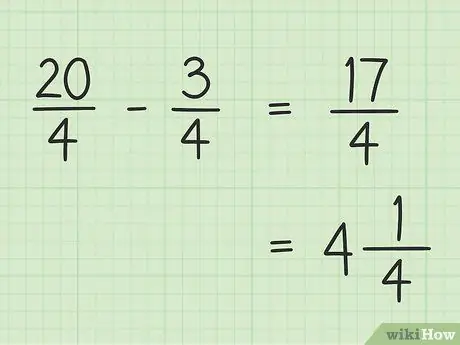
Βήμα 5. Γράψτε το τελικό σας αποτέλεσμα
Το τελικό σας αποτέλεσμα είναι 17/4. Εάν θέλετε να το γράψετε ως μικτός αριθμός, διαιρέστε το 17 με 4, έτσι ώστε το αποτέλεσμα να είναι 4 και το υπόλοιπο 1, έτσι ώστε το τελικό σας 17/4 να ισούται με 4.
Μέθοδος 6 από 6: Αφαίρεση μεταβλητών
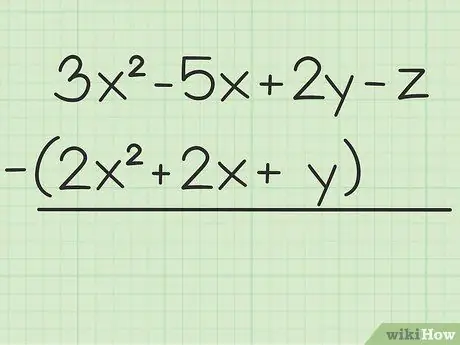
Βήμα 1. Γράψτε το πρόβλημα που θέλετε να λύσετε
Για παράδειγμα, η ακόλουθη ερώτηση: 3x2 - 5x + 2y - z - (2x2 + 2x + y). Γράψτε το πρώτο σύνολο μεταβλητών στο δεύτερο.
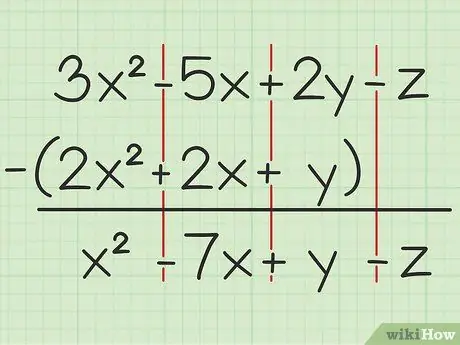
Βήμα 2. Αφαιρέστε τις ίδιες μεταβλητές
Εάν συναντήσετε μια μεταβλητή, μπορείτε να προσθέσετε ή να αφαιρέσετε μόνο την ίδια μεταβλητή και η οποία είναι γραμμένη με τον ίδιο βαθμό τετραγώνου. Αυτό σημαίνει ότι μπορείτε να αφαιρέσετε 4 φορές2 από 7x2, αλλά δεν μπορεί να αφαιρέσει 4x από 4y. Έτσι, μπορείτε να σπάσετε το πρόβλημα ως εξής:
- 3x2 - 2x2 = x2
- -5x -2x = -7x
- 2y - y = y
- -z -0 = -z
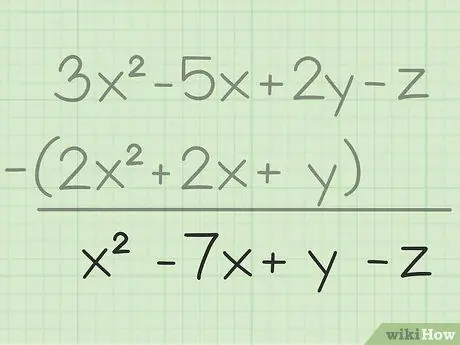
Βήμα 3. Γράψτε το τελικό σας αποτέλεσμα
Έχετε αφαιρέσει όλες τις ίδιες μεταβλητές, το μόνο που έχετε να κάνετε είναι να γράψετε το τελικό σας αποτέλεσμα το οποίο θα περιέχει όλες τις μεταβλητές που έχετε αφαιρέσει. Εδώ είναι το τελικό αποτέλεσμα:






