- Συγγραφέας Jason Gerald gerald@how-what-advice.com.
- Public 2024-01-19 22:12.
- Τελευταία τροποποίηση 2025-01-23 12:15.
Οι μαθητές που είναι ακόμα πολύ νέοι συχνά δυσκολεύονται να κατανοήσουν την έννοια της αφαίρεσης. Εάν είστε δάσκαλος και θέλετε να διδάξετε την έννοια της αφαίρεσης στους μαθητές, προσπαθήστε να εκπροσωπήσετε την έννοια με έναν τρόπο ενδιαφέροντα και πιο κατανοητό για τους μαθητές. Αφού εξηγήσετε τις βασικές έννοιες της αφαίρεσης, δοκιμάστε να προχωρήσετε στην έννοια της διψήφιας αφαίρεσης. Μόλις οι μαθητές το κατακτήσουν καλά, προσπαθήστε να εξηγήσετε διάφορες έννοιες που μπορούν να χρησιμοποιήσουν για να λύσουν προβλήματα αφαίρεσης, όπως το Common Core.
Βήμα
Μέθοδος 1 από 4: Διδασκαλία της αφαίρεσης μέσω αντικειμένων ή εικόνων

Βήμα 1. Γράψτε ή παρουσιάστε προφορικά ένα πρόβλημα ιστορίας που περιέχει πρόβλημα αφαίρεσης στους μαθητές:
Υπάρχουν 8 πορτοκάλια στο τραπέζι, 3 πορτοκάλια τρώγονται από τον Τζόρνταν. Πόσα πορτοκάλια έχουν μείνει;
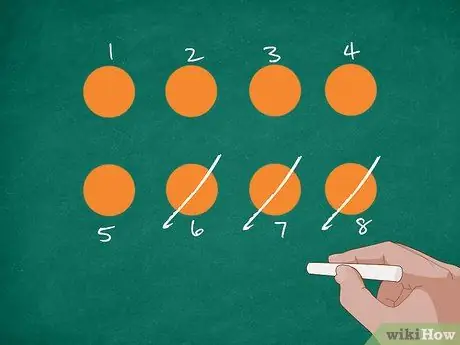
Βήμα 2. Αντιπροσωπεύστε το πρόβλημα με εικόνες
Αρχικά, σχεδιάστε 8 πορτοκαλί κύκλους στον πίνακα ή ένα κομμάτι χαρτί. Μετά από αυτό, ζητήστε από τους μαθητές να μετρήσουν τον αριθμό και να επισημάνουν κάθε κύκλο με έναν αριθμό. Διαγράψτε 3 κύκλους εξηγώντας ότι ο Τζόρνταν έφαγε 3 πορτοκάλια. Ρωτήστε τους μαθητές πόσα πορτοκάλια έχουν απομείνει τώρα.
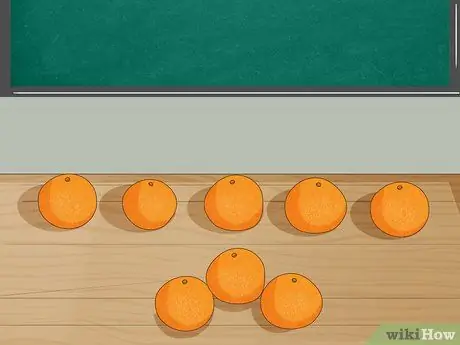
Βήμα 3. Αντιπροσωπεύστε το πρόβλημα με αντικείμενα
Τοποθετήστε 8 πορτοκάλια στο τραπέζι και ζητήστε από τους μαθητές να μετρήσουν τον αριθμό. Μετά από αυτό, πάρτε 3 πορτοκάλια από το τραπέζι ενώ εξηγείτε ότι ο Τζόρνταν έφαγε 3 πορτοκάλια. Ζητήστε από τους μαθητές να μετρήσουν τον αριθμό των πορτοκαλιών που απομένουν.

Βήμα 4. Γράψτε την εξίσωση
Εξηγήστε ότι τα προβλήματα της ιστορίας μπορούν επίσης να αναπαρασταθούν μέσω μιας εξίσωσης. Βεβαιωθείτε ότι τους καθοδηγείτε πάντα στη διαδικασία μετατροπής προβλημάτων ιστορίας σε μαθηματικές εξισώσεις.
- Ρωτήστε πόσα πορτοκάλια υπάρχουν στο τραπέζι. Γράψτε τον αριθμό «8» στον πίνακα.
- Ρωτήστε πόσα πορτοκάλια έφαγε ο Τζόρνταν. Γράψτε τον αριθμό «3» στον πίνακα.
- Ρωτήστε τους μαθητές εάν αυτό είναι πρόβλημα πρόσθεσης ή αφαίρεσης. Γράψτε ένα σύμβολο "-" μεταξύ των αριθμών "8" και "3".
- Ζητήστε από τους μαθητές να αναζητήσουν απαντήσεις στην εξίσωση «8-3». Γράψτε ένα σύμβολο "=" ακολουθούμενο από τον αριθμό "5"
Μέθοδος 2 από 4: Διδασκαλία της αφαίρεσης με τη μέθοδο της αντίστροφης μέτρησης στην αριθμητική γραμμή

Βήμα 1. Γράψτε ή παρουσιάστε προφορικά ένα πρόβλημα ιστορίας που περιέχει πρόβλημα αφαίρεσης στους μαθητές:
Υπάρχουν 10 σκυλιά στο pet shop, 6 από τα οποία έχουν υιοθετηθεί από τους νέους ιδιοκτήτες τους. Πόσα σκυλιά έχουν μείνει στο pet shop;
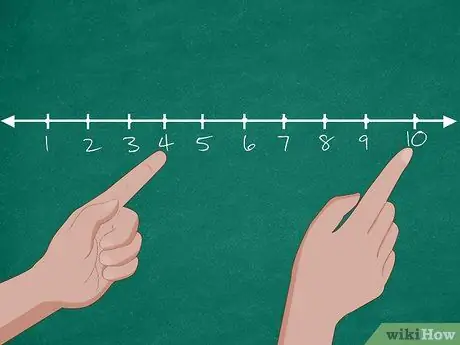
Βήμα 2. Χρησιμοποιήστε τη βοήθεια μιας αριθμητικής γραμμής για να λύσετε το πρόβλημα
Αρχικά, σχεδιάστε μια αριθμητική γραμμή που περιέχει τους αριθμούς 0-10 στον πίνακα. Μετά από αυτό, ζητήστε από τους μαθητές να αναφέρουν τον αριθμό των σκύλων στο pet shop. Αφού απαντήσουν οι μαθητές, κυκλώστε τον αριθμό «10» στον πίνακα. Στη συνέχεια, ρωτήστε ξανά πόσα σκυλιά έχουν υιοθετηθεί. Εάν οι μαθητές απαντήσουν "6", ζητήστε τους να μετρήσουν αντίστροφα 6 αριθμούς από 10 (9, 8, 7, 6, 5, 4) μέχρι να φτάσουν στον αριθμό "4". Μετά από αυτό, ρωτήστε ξανά πόσα σκυλιά έχουν μείνει στο κατάστημα κατοικίδιων ζώων.

Βήμα 3. Γράψτε την εξίσωση
Εξηγήστε ότι τα προβλήματα της ιστορίας μπορούν επίσης να αναπαρασταθούν μέσω μιας εξίσωσης. Βεβαιωθείτε ότι τους καθοδηγείτε πάντα στη διαδικασία μετατροπής προβλημάτων ιστορίας σε μαθηματικές εξισώσεις.
- Ρωτήστε πόσα σκυλιά υπάρχουν στο κατάστημα κατοικίδιων ζώων. Γράψτε τον αριθμό «10» στον πίνακα.
- Ρωτήστε πόσα σκυλιά υιοθετήθηκαν. Γράψτε τον αριθμό «6» στον πίνακα.
- Ρωτήστε τους μαθητές εάν αυτό είναι πρόβλημα πρόσθεσης ή αφαίρεσης. Γράψτε ένα σύμβολο "-" μεταξύ των αριθμών "10" και "6".
- Ζητήστε από τους μαθητές να αναζητήσουν απαντήσεις στην εξίσωση «10-6». Γράψτε ένα σύμβολο "=" ακολουθούμενο από τον αριθμό "4"
Μέθοδος 3 από 4: Διδασκαλία αφαίρεσης μέσω οικογενειακών εννοιών γεγονότων

Βήμα 1. Εισαγάγετε την έννοια της οικογένειας γεγονότων στους μαθητές
Στην πραγματικότητα, μια οικογένεια γεγονότων είναι μια ομάδα μαθηματικών προβλημάτων που αποτελούνται από τους ίδιους αριθμούς. Για παράδειγμα, οι αριθμοί 10, 3 και 7 αποτελούν μια οικογένεια γεγονότων. Οι τρεις αριθμοί μπορούν να προστεθούν ή να αφαιρεθούν με διαφορετικούς τρόπους. Μπορείτε να δημιουργήσετε δύο εξισώσεις χρησιμοποιώντας μόνο αυτούς τους 3 αριθμούς:
- 10-3=7
- 10-7=3
- 7+3=10
- 3+7=10

Βήμα 2. Γράψτε ή παρουσιάστε προφορικά ένα πρόβλημα ιστορίας που περιέχει πρόβλημα αφαίρεσης στους μαθητές:
Έχω 7 καραμέλες. Αν φάω 3 καραμέλες, πόσες καραμέλες μένουν;

Βήμα 3. Χρησιμοποιήστε την έννοια της οικογένειας γεγονότων για να λύσετε το πρόβλημα
Καθοδήγηση των μαθητών στη διαδικασία βήμα προς βήμα:
- Ρωτήστε τους μαθητές ποιο πρόβλημα θα ήθελαν να λύσουν. Γράψτε "7-3 =;" στον μαυροπίνακα.
- Ζητήστε τους να προσδιορίσουν το τρίτο μέλος της ομάδας οικογένειας γεγονότων. Γράψτε τις ακόλουθες εξισώσεις στον πίνακα: "3+_ = 7". "_+3 = 7"; "; "7 -_ = 3"; και 7-3 = _”Στη συνέχεια, ζητήστε από τους μαθητές να διαβάσουν τα αποτελέσματα και να συμπληρώσουν το πρόβλημα με τις απαντήσεις που έδωσαν.
Μέθοδος 4 από 4: Εισαγωγή κοινών βασικών εννοιών
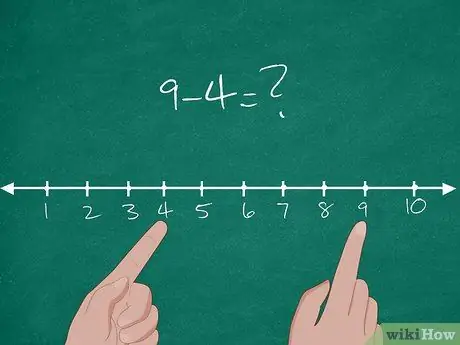
Βήμα 1. Διδάξτε την έννοια της αφαίρεσης στον Κοινό Πυρήνα
Στην πραγματικότητα, το Common Core είναι ένα νέο πρότυπο μάθησης που εφαρμόζεται από τα περισσότερα κράτη στην Αμερική. Στο Common Core, η βασική έννοια της αφαίρεσης εξηγείται από την απόσταση μεταξύ δύο αριθμών. Για να εξηγήσετε την έννοια στους μαθητές, δοκιμάστε να σχεδιάσετε μια αριθμητική γραμμή που περιέχει τους αριθμούς 1-10 στον πίνακα.
- Μετά από αυτό, δώστε ένα βασικό πρόβλημα αφαίρεσης στους μαθητές: 9-4 =;.
- Βρείτε τη θέση του αριθμού 4 στην αριθμητική γραμμή. Εξηγήστε στους μαθητές ότι αυτή η τοποθεσία είναι η αφετηρία τους.
- Βρείτε τη θέση του αριθμού 9 στην αριθμητική γραμμή. Εξηγήστε στους μαθητές ότι η τοποθεσία είναι ο τελικός προορισμός.
- Μετά από αυτό, ζητήστε από τους μαθητές να μετρήσουν ή να υπολογίσουν την απόσταση μεταξύ των δύο αριθμών: «5, 6, 7, 8, 9».
- Η απόσταση μεταξύ των δύο αριθμών είναι 5. Έτσι, 9-4 = 5.
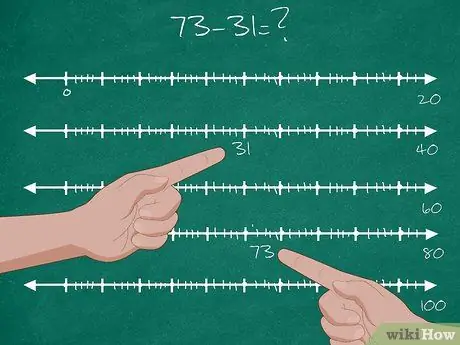
Βήμα 2. Βάλτε τους μαθητές να λύσουν το διψήφιο πρόβλημα αφαίρεσης
Εξηγήστε στους μαθητές ότι θα υπάρχουν δύο σημεία που πρέπει να σταματήσουν πριν φτάσουν στον προορισμό τους.
- Δώστε στους μαθητές ένα διψήφιο πρόβλημα αφαίρεσης: 73-31 =;.
- Βρείτε τη θέση του αριθμού 31 στην αριθμητική γραμμή. Αυτό είναι το σημείο εκκίνησης.
- Βρείτε τη θέση του αριθμού 73 στην αριθμητική γραμμή. Αυτός είναι ο τελικός στόχος.
- "Σταματήστε" στο πρώτο δέκατο μετά τα 31. Έτσι, η πρώτη σας στάση είναι 40. Μετά από αυτό, μετρήστε την απόσταση μεταξύ 31 και 40 και γράψτε την απάντηση: 9.
- "Σταματήστε" στα δέκατα που είναι πιο κοντά στο 73. Έτσι, η δεύτερη στάση σας είναι 70. Στη συνέχεια, μετρήστε την απόσταση μεταξύ 40 (πρώτη στάση) και 70 (δεύτερη στάση) και γράψτε την απάντηση: 30.
- "Μετακίνηση" από 70 (δεύτερη στάση) στον τελικό προορισμό σας (73). Μετρήστε την απόσταση μεταξύ τους και γράψτε την απάντηση: 3.
- Προσθέστε αυτά τα τρία αποτελέσματα μαζί: 9+30+3 = 42. Έτσι, 73-31 = 42.

Βήμα 3. Βάλτε τους μαθητές να λύσουν το τριψήφιο πρόβλημα αφαίρεσης
Κατά την επίλυση διψήφιων προβλημάτων αφαίρεσης, εξηγήστε στους μαθητές ότι αυτό που θα αυξηθεί δεν είναι μόνο οι στάσεις, αλλά και η απόσταση μεταξύ κάθε ενδιάμεσης στάσης.
- Δώστε στους μαθητές ένα τριψήφιο πρόβλημα αφαίρεσης: 815-398 =;.
- Βρείτε τη θέση του αριθμού 398 στην αριθμητική γραμμή. Αυτό είναι το σημείο εκκίνησης.
- Βρείτε τη θέση του αριθμού 815 στην αριθμητική γραμμή. Αυτός είναι ο τελικός στόχος.
- "Σταματήστε" στο πρώτο δέκατο μετά το 398. Έτσι, η πρώτη σας στάση είναι 400. Μετρήστε την απόσταση μεταξύ 398 και 400 και γράψτε την απάντηση: 2.
- "Σταματήστε" στα δέκατα που είναι πιο κοντά στο 815. Άρα η δεύτερη στάση σας είναι 800. Μετρήστε την απόσταση μεταξύ 400 και 800 και γράψτε την απάντηση: 400.
- "Σταματήστε" στα δέκατα που είναι πιο κοντά στο 815. Έτσι, η τρίτη στάση σας είναι 810. Μετρήστε την απόσταση μεταξύ 800 και 810 και γράψτε την απάντηση: 10.
- "Μετακινήστε" από την τρίτη στάση στον τελικό προορισμό σας, που είναι ο αριθμός 815. Μετρήστε την απόσταση και γράψτε την απάντηση: 5.
- Προσθέστε όλους τους αριθμούς που λαμβάνετε: 2+400+10+5 = 417. Έτσι, 815-398-417.






