- Συγγραφέας Jason Gerald gerald@how-what-advice.com.
- Public 2024-02-01 14:12.
- Τελευταία τροποποίηση 2025-01-23 12:15.
Όλοι μπορούν να μάθουν Μαθηματικά είτε βρίσκονται ήδη σε ανώτερο στάδιο στο σχολείο είτε θέλουν απλώς να βελτιώσουν ξανά τα βασικά. Αφού συζητήσετε πώς να γίνετε καλός μαθητής στα Μαθηματικά, αυτό το άρθρο θα σας διδάξει τις βασικές μαθηματικές προόδους και θα σας δώσει τα βασικά στοιχεία που θα πρέπει να μάθετε σε κάθε πρακτική. Στη συνέχεια, αυτό το άρθρο θα συζητήσει τα βασικά της εκμάθησης της αριθμητικής, τα οποία θα βοηθήσουν τόσο τα παιδιά του δημοτικού όσο και όλους όσους θέλουν να μάθουν τα βασικά αυτού του τομέα της επιστήμης.
Βήμα
Μέρος 1 από 6: Κλειδιά για να γίνετε καλός μαθητής μαθηματικών

Βήμα 1. Εμφανιστείτε στην τάξη
Όταν χάνετε το μάθημα, θα πρέπει να μάθετε έννοιες από συμμαθητές ή από το σχολικό σας βιβλίο. Ποτέ δεν θα λάβετε μια περίληψη κειμένου από έναν φίλο όσο παίρνετε από τον δάσκαλό σας.
- Ελα στην τάξη στην ώρα σου. Αντ 'αυτού, φτάστε λίγο νωρίτερα και ανοίξτε το σημειωματάριό σας στο σωστό μέρος, ανοίξτε το σχολικό σας βιβλίο και βγάλτε την αριθμομηχανή σας ώστε να είστε έτοιμοι να ξεκινήσετε όταν ο δάσκαλός σας είναι έτοιμος να διδάξει.
- Απαλλαγείτε μόνο εάν είστε άρρωστοι. Εάν πραγματικά χάνετε το μάθημα, ζητήστε από τους συμμαθητές σας να μάθουν για τι μιλούσε ο δάσκαλος και ποια εργασία είχε δοθεί.

Βήμα 2. Συνεργαστείτε με τον δάσκαλό σας
Εάν ο δάσκαλός σας εργάζεται πάνω σε ένα πρόβλημα μπροστά στην τάξη, συνεργαστείτε με τον δάσκαλο δουλεύοντας το πρόβλημα στο σημειωματάριό σας.
- Βεβαιωθείτε ότι οι σημειώσεις σας είναι σαφείς και ευανάγνωστες. Μην γράφετε μόνο ερωτήσεις. Γράψτε επίσης οτιδήποτε λέει ο δάσκαλος που μπορεί να βελτιώσει την κατανόησή σας για τις έννοιες που εξηγούνται.
- Συμπληρώστε τα δείγματα ερωτήσεων που δίνονται από τον καθηγητή σας. Καθώς ο δάσκαλος περπατά στην τάξη καθώς εργάζεστε, απαντήστε στις ερωτήσεις που τίθενται.
- Συμμετέχετε όταν ο δάσκαλος λύσει ένα πρόβλημα. Μην περιμένετε να σας καλέσει ο δάσκαλος. Προσφέρετε να απαντήσετε όταν γνωρίζετε την απάντηση και σηκώστε το χέρι σας για να κάνετε μια ερώτηση εάν δεν είστε σίγουροι για το υλικό που διδάσκεται.

Βήμα 3. Κάντε την εργασία σας την ίδια ημέρα που θα δοθούν οι εργασίες σας
Εάν κάνετε την εργασία σας την ίδια μέρα, η ιδέα είναι ακόμα φρέσκια στο μυαλό σας. Μερικές φορές, δεν μπορείτε να ολοκληρώσετε την εργασία σας την ίδια μέρα. Βεβαιωθείτε ότι η εργασία σας έχει ολοκληρωθεί πριν πάτε στο μάθημα.

Βήμα 4. Εργαστείτε εκτός τάξης εάν χρειάζεστε βοήθεια
Επισκεφθείτε τον δάσκαλό σας κατά τη διάρκεια των διαλειμμάτων ή κατά τις ώρες γραφείου.
- Εάν έχετε ένα Μαθηματικό Κέντρο στο σχολείο σας, μάθετε τις ώρες λειτουργίας του και ζητήστε βοήθεια.
- Γίνετε μέλος μιας ομάδας μελέτης. Μια καλή ομάδα μελέτης αποτελείται γενικά από 4 ή 5 άτομα με διαφορετικά επίπεδα ικανότητας. Εάν είστε μαθητής «Γ» στα Μαθηματικά, ενταχθείτε σε μια ομάδα 2 ή 3 μαθητών με βαθμούς «Α» ή «Β», ώστε να βελτιώσετε τις δεξιότητές σας. Αποφύγετε να συμμετάσχετε σε μια ομάδα μαθητών των οποίων οι βαθμοί είναι χαμηλότεροι από τους δικούς σας.
Μέρος 2 από 6: Εκμάθηση μαθηματικών στο σχολείο

Βήμα 1. Ξεκινήστε με αριθμητική
Στα περισσότερα σχολεία, οι μαθητές μαθαίνουν αριθμητική στο δημοτικό σχολείο. Η αριθμητική καλύπτει τα βασικά της προσθήκης, αφαίρεσης, πολλαπλασιασμού και διαίρεσης.
- Κάντε πρακτικές ερωτήσεις. Το να κάνετε αριθμητικά προβλήματα ξανά και ξανά είναι ο καλύτερος τρόπος για να απομνημονεύσετε σωστά τα βασικά. Αναζητήστε λογισμικό που μπορεί να σας προσφέρει μια μεγάλη ποικιλία διαφορετικών μαθηματικών προβλημάτων για εργασία. Επίσης, αναζητήστε προβλήματα με τα χρονικά πλαίσια για να βελτιώσετε την ταχύτητά σας.
- Μπορείτε επίσης να βρείτε αριθμητικά προβλήματα στο διαδίκτυο και μπορείτε να κάνετε λήψη αριθμητικών εφαρμογών στην κινητή συσκευή σας.

Βήμα 2. Συνεχίστε με την προ-άλγεβρα
Αυτή η άσκηση θα σας παρέχει τα βασικά στοιχεία που θα χρειαστείτε για να λύσετε προβλήματα άλγεβρας αργότερα.
- Μάθετε για κλάσματα και δεκαδικά ψηφία. Θα μάθετε να προσθέτετε, αφαιρείτε, πολλαπλασιάζετε και διαιρείτε κλάσματα και δεκαδικά. Όσον αφορά τα κλάσματα, θα μάθετε πώς να αφαιρείτε κλάσματα και να μεταφράζετε συνδυασμένους αριθμούς. Όσον αφορά τα δεκαδικά, θα κατανοήσετε τις αξίες των τόπων και θα μπορείτε να χρησιμοποιήσετε δεκαδικούς σε προβλήματα ιστορίας.
- Μάθετε για τις αναλογίες, τις αναλογίες και τα ποσοστά. Αυτές οι έννοιες θα σας βοηθήσουν να μάθετε να κάνετε συγκρίσεις.
- Εισαγάγετε τον εαυτό σας στη βασική γεωμετρία. Θα μάθετε τρισδιάστατα σχήματα και έννοιες. Θα μάθετε επίσης έννοιες όπως εμβαδόν, περίμετρο, όγκο και επιφάνεια, καθώς και πληροφορίες σχετικά με παράλληλες και κάθετες γραμμές και γωνίες.
- Κατανόηση ορισμένων βασικών στατιστικών. Στην προ-άλγεβρα, η εισαγωγή σας στα στατιστικά περιλαμβάνει γενικά εικόνες όπως γραφήματα, διαγράμματα διασποράς, διαγράμματα γραμματοσήμων και ιστογράμματα.
- Μάθετε τα βασικά της άλγεβρας. Αυτό περιλαμβάνει έννοιες όπως επίλυση απλών εξισώσεων που περιέχουν μεταβλητές, εκμάθηση για ιδιότητες όπως η ιδιότητα κατανομής, σχεδίαση απλών εξισώσεων και επίλυση ανισοτήτων.
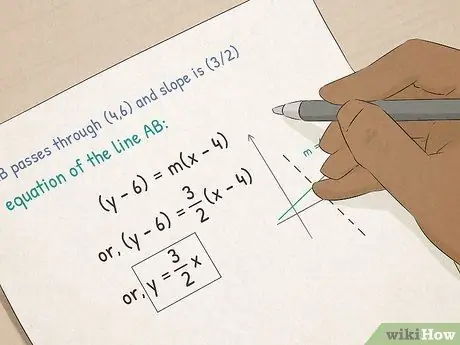
Βήμα 3. Προχωρήστε στην Άλγεβρα Ι
Στο πρώτο έτος της άλγεβρας, θα μάθετε για τα βασικά σύμβολα που περιλαμβάνονται στην άλγεβρα. Θα μάθετε επίσης να:
- Λύστε εξισώσεις και ανισότητες που περιέχουν μεταβλητές. Θα μάθετε πώς να λύσετε αυτά τα προβλήματα σε χαρτί και πώς να τα λύσετε με εικόνες.
- Λύστε προβλήματα ιστορίας. Θα εκπλαγείτε πόσα καθημερινά προβλήματα θα αντιμετωπίσετε στο μέλλον που απαιτούν την ικανότητα επίλυσης αλγεβρικών προβλημάτων ιστορίας. Για παράδειγμα, θα χρησιμοποιούσατε άλγεβρα για να μάθετε το επιτόκιο που κερδίζετε στον τραπεζικό λογαριασμό ή την επένδυσή σας. Μπορείτε επίσης να χρησιμοποιήσετε την άλγεβρα για να καταλάβετε πόσο καιρό πρέπει να ταξιδέψετε με βάση την ταχύτητα του αυτοκινήτου σας.
- Εργασία με εκθέτες. Όταν ξεκινάτε την επίλυση πολυωνυμικών εξισώσεων (εκφράσεις που περιέχουν αριθμούς και μεταβλητές), θα καταλάβετε πώς να χρησιμοποιείτε εκθέτες. Αυτό θα περιλαμβάνει πιθανώς ασκήσεις με επιστημονική σημειογραφία. Μόλις κατακτήσετε εκθέτες, μπορείτε να μάθετε να προσθέτετε, αφαιρείτε, πολλαπλασιάζετε και διαιρείτε πολυώνυμες εκφράσεις.
- Λύστε προβλήματα τετραγωνικής και τετραγωνικής ρίζας. Καθώς κατακτάτε αυτό το θέμα, θα μπορείτε να απομνημονεύσετε τα τετράγωνα πολλών αριθμών. Θα μπορείτε επίσης να εργαστείτε με εξισώσεις που έχουν τετραγωνικές ρίζες.
- Κατανόηση συναρτήσεων και γραφημάτων. Στην άλγεβρα, θα μάθετε για γραφικές εξισώσεις. Θα μάθετε πώς να υπολογίζετε την κλίση μιας γραμμής, πώς να τοποθετείτε μια εξίσωση σε μορφή σημείου κλίσης και πώς να υπολογίζετε τη φέτα x-και-y μιας γραμμής χρησιμοποιώντας τη φόρμα κλίσης κλίσης.
- Μάθετε το σύστημα των εξισώσεων. Μερικές φορές, σας δίνονται 2 διαφορετικές εξισώσεις με τις μεταβλητές x και y και πρέπει να λύσετε για x ή y και για τις δύο εξισώσεις. Ευτυχώς, θα μάθετε πολλά κόλπα για την επίλυση αυτών των εξισώσεων, όπως η γραφική παράσταση, η αντικατάσταση και η προσθήκη.

Βήμα 4. Μελετήστε τη γεωμετρία
Στη γεωμετρία, θα μάθετε για τις ιδιότητες των γραμμών, τμημάτων, γωνιών και σχημάτων.
- Θα απομνημονεύσετε μια σειρά θεωρημάτων και συμπερασμάτων που θα σας βοηθήσουν να κατανοήσετε τους κανόνες της γεωμετρίας.
- Θα μάθετε πώς να υπολογίζετε το εμβαδόν ενός κύκλου, πώς να χρησιμοποιείτε το Πυθαγόρειο θεώρημα και πώς να βρίσκετε τη σχέση μεταξύ των γωνιών και των πλευρών ενός ειδικού τριγώνου.
- Θα δείτε πολλές ερωτήσεις γεωμετρίας σε μελλοντικές τυποποιημένες δοκιμές όπως τα SAT, ACT και GRE.
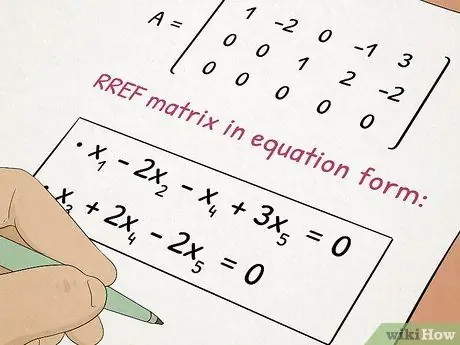
Βήμα 5. Πάρτε τάξη Άλγεβρα II
Η Άλγεβρα II βασίζεται στις έννοιες που μάθατε στην Άλγεβρα Ι ενώ προσθέτετε σε πολύπλοκα θέματα όπως τετραγωνικές εξισώσεις και πίνακες.
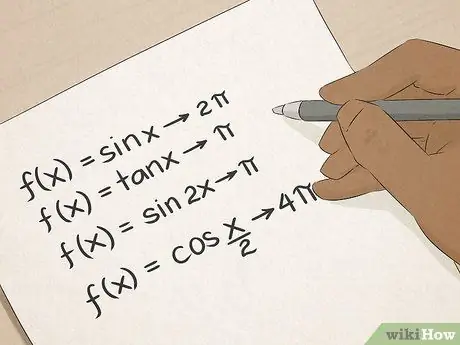
Βήμα 6. Κύρια τριγωνομετρία
Γνωρίζετε τριγωνομετρικούς όρους: ημιτόνο, συνημίτονο, εφαπτομένη κ.ο.κ. Η τριγωνομετρία θα σας διδάξει πολλούς πρακτικούς τρόπους υπολογισμού γωνιών και μήκους γραμμών, και αυτές οι δεξιότητες θα είναι ανεκτίμητες για άτομα που εργάζονται σε οικοδομές, αρχιτεκτονική, μηχανική ή τοπογραφία.
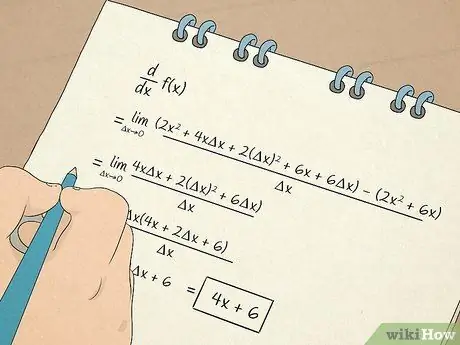
Βήμα 7. Εκτελέστε υπολογισμούς υπολογισμού
Ο Λογισμός μπορεί να ακούγεται εκφοβιστικό, αλλά είναι ένα υπέροχο εργαλείο για την κατανόηση είτε της συμπεριφοράς των αριθμών είτε του κόσμου γύρω σας.
- Ο Λογισμός θα σας διδάξει λειτουργίες και όρια. Θα δείτε την αριθμητική συμπεριφορά χρήσιμων συναρτήσεων, συμπεριλαμβανομένων των e^x και λογαριθμικών συναρτήσεων.
- Θα μάθετε επίσης πώς να υπολογίζετε και να εργάζεστε με παράγωγα. Το πρώτο παράγωγο σας δίνει πληροφορίες με βάση την κλίση της εφαπτομένης γραμμής σε μια εξίσωση. Για παράδειγμα, ένα παράγωγο σας λέει τον ρυθμό με τον οποίο κάτι αλλάζει σε μια μη γραμμική κατάσταση. Το δεύτερο παράγωγο θα σας πει εάν η συνάρτηση αυξάνεται ή μειώνεται σε ένα συγκεκριμένο διάστημα, ώστε να μπορείτε να καθορίσετε την κοίλοτητα μιας συνάρτησης.
- Τα ολοκληρωμένα θα σας διδάξουν πώς να υπολογίσετε το εμβαδόν κάτω από μια καμπύλη καθώς και τον όγκο του.
- Ο λογισμός στο λύκειο τελειώνει γενικά σε ακολουθίες και ακολουθίες. Αν και οι μαθητές δεν θα δουν πολλές εφαρμογές για κυκλώματα, τα κυκλώματα είναι σημαντικά για όσους μελετούν διαφορικές εξισώσεις.
Μέρος 3 από 6: Βασικές αρχές μαθηματικών-Προσθήκη κύριου

Βήμα 1. Ξεκινήστε με γεγονότα "+1"
Η προσθήκη 1 σε έναν αριθμό σας οδηγεί στον μεγαλύτερο αριθμό στην αριθμητική γραμμή. Για παράδειγμα, 2 + 1 = 3.
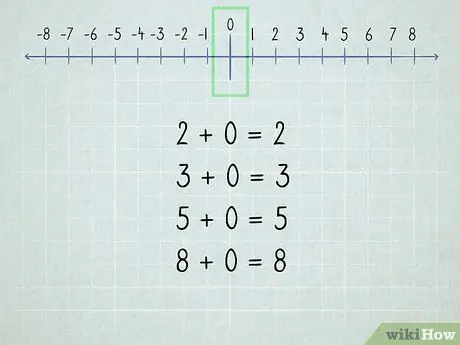
Βήμα 2. Κατανοήστε το μηδέν
Όλοι οι αριθμοί που προστίθενται στο μηδέν είναι ο ίδιος αριθμός επειδή "μηδέν" σημαίνει "κανένας".

Βήμα 3. Μάθετε διπλούς αριθμούς
Οι πολλαπλοί αριθμοί είναι ένα πρόβλημα που περιλαμβάνει την πρόσθεση δύο ίσων αριθμών. Για παράδειγμα, 3 + 3 = 6 είναι ένα παράδειγμα εξίσωσης που περιλαμβάνει πολλαπλούς αριθμούς.

Βήμα 4. Χρησιμοποιήστε τη χαρτογράφηση για να μάθετε για άλλες λύσεις προσθήκης
Στο παρακάτω παράδειγμα, μαθαίνετε χαρτογραφώντας τι συμβαίνει όταν προσθέτετε 3 στα 5, 2 και 1. Δοκιμάστε μόνοι σας το πρόβλημα "προσθήκη κατά 2".

Βήμα 5. Συνεχίστε μέχρι ο αριθμός να είναι πάνω από 10
Μάθετε να προσθέτετε 3 αριθμούς μαζί για να λάβετε έναν αριθμό μεγαλύτερο από 10.
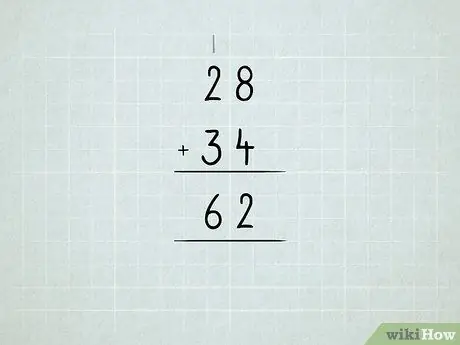
Βήμα 6. Προσθέστε τους μεγαλύτερους αριθμούς
Μάθετε για την ομαδοποίηση των μονάδων σε δεκάδες, δεκάδες σε εκατοντάδες και ούτω καθεξής.
- Προσθέστε πρώτα τους αριθμούς στη δεξιά στήλη. 8 + 4 = 12, που σημαίνει ότι έχετε 1 αριθμό 10 και 2 αριθμό 1. Γράψτε τον αριθμό 2 κάτω από τη στήλη μονάδων.
-
Γράψτε τον αριθμό 1 στη στήλη των δεκάδων.
-
Προσθέστε τη στήλη των δεκάδων στο σύνολό της.
Μέρος 4 από 6: Μαθηματικές βασικές αρχές-στρατηγικές μείωσης

Βήμα 1. Ξεκινήστε με "1 ψηφίο προς τα πίσω
Η αφαίρεση 1 από έναν αριθμό σας επιστρέφει 1 αριθμό. Για παράδειγμα, 4 - 1 = 3.

Βήμα 2. Μάθετε να αφαιρείτε διπλούς αριθμούς
Για παράδειγμα, προσθέτετε τους αριθμούς 5 + 5 για να πάρετε 10. Απλώς γράψτε την εξίσωση προς τα πίσω για να πάρετε 10 - 5 = 5.
- Αν 5 + 5 = 10, τότε 10 - 5 = 5.
-
Αν 2 + 2 = 4, τότε 4 - 2 = 2.

Βήμα 3. Απομνημονεύστε την οικογένεια γεγονότων
Ως παράδειγμα:
- 3 + 1 = 4
- 1 + 3 = 4
- 4 - 1 = 3
- 4 - 3 = 1

Βήμα 4. Βρείτε τους αριθμούς που λείπουν
Για παράδειγμα, _ + 1 = 6 (η απάντηση είναι 5).

Βήμα 5. Απομνημονεύστε το γεγονός της αφαίρεσης στο 20

Βήμα 6. Εξασκηθείτε στην αφαίρεση μονοψήφιων αριθμών από διψήφιους αριθμούς χωρίς δανεισμό
Αφαιρέστε τους αριθμούς στη στήλη one και μειώστε τους αριθμούς στη στήλη των δεκάδων.
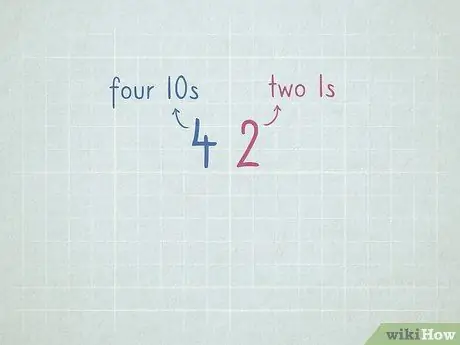
Βήμα 7. Εξασκηθείτε στην αξία τόπου για να προετοιμαστείτε για αφαίρεση με δανεισμό
- 32 = 3 αριθμοί 10 και 2 αριθμοί 1.
- 64 = 6 αριθμοί 10 και 4 αριθμοί 1.
- 96 = _ αριθμός 10 και _ αριθμός 1.
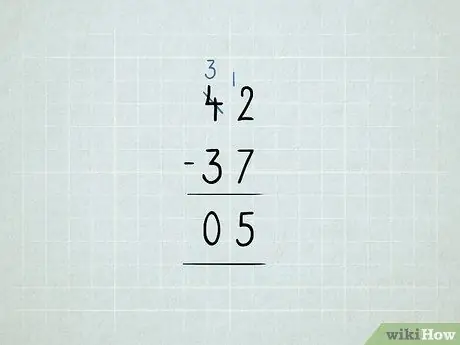
Βήμα 8. Αφαιρέστε με δανεισμό
- Θέλετε να αφαιρέσετε 42 - 37. Ξεκινάτε προσπαθώντας να αφαιρέσετε 2 - 7 στη στήλη μονάδων. Αποδείχθηκε, δεν λειτούργησε!
-
Δανειστείτε τον αριθμό 10 από τη στήλη των δεκάδων και τοποθετήστε τον στη στήλη μονάδες. Τώρα έχετε 3 10 αντί για 4 10. Τώρα έχετε 12 1 αντί για 2 1.
-
Αφαιρέστε πρώτα τη στήλη των μονάδων σας: 12 - 7 = 5. Στη συνέχεια, ελέγξτε τη στήλη των δεκάδων. Δεδομένου ότι 3 - 3 = 0, δεν χρειάζεται να γράψετε τον αριθμό 0. Η απάντησή σας είναι 5.
Μέρος 5 από 6: Βασικές αρχές των μαθηματικών-Κύριος πολλαπλασιασμός

Βήμα 1. Ξεκινήστε με τον αριθμό 1 και τον αριθμό 0
Όλοι οι αριθμοί που πολλαπλασιάζονται με 1 είναι ίδιοι με τον ίδιο τον αριθμό. Οποιοσδήποτε αριθμός πολλαπλασιασμένος με 0 ισούται με μηδέν.

Βήμα 2. Απομνημονεύστε τον πίνακα πολλαπλασιασμού

Βήμα 3. Εξασκηθείτε με μονοψήφια προβλήματα πολλαπλασιασμού

Βήμα 4. Πολλαπλασιάστε τον διψήφιο αριθμό με τον 1ψήφιο αριθμό
- Πολλαπλασιάστε τον κάτω δεξιό αριθμό με τον επάνω δεξιό αριθμό.
-
Πολλαπλασιάστε τον κάτω δεξιό αριθμό με τον επάνω αριστερό αριθμό.
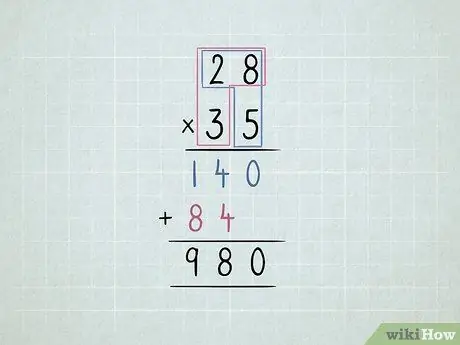
Βήμα 5. Πολλαπλασιάστε 2 διψήφιους αριθμούς
- Πολλαπλασιάστε τον κάτω δεξιό αριθμό με τον επάνω δεξιό αριθμό και στη συνέχεια με τον επάνω αριστερό αριθμό.
-
Μετακινήστε τη δεύτερη σειρά ένα ψηφίο προς τα αριστερά.
- Πολλαπλασιάστε τον κάτω αριστερό αριθμό με τον επάνω δεξιό αριθμό και στη συνέχεια τον επάνω αριστερό αριθμό.
-
Προσθέστε όλες τις στήλες.
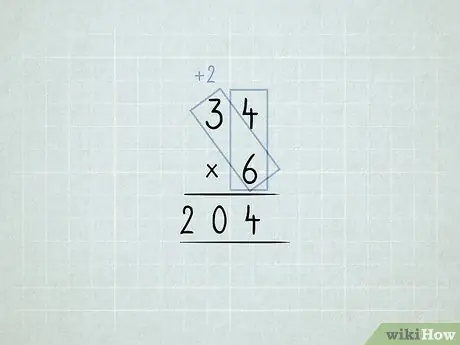
Βήμα 6. Πολλαπλασιάστε και ομαδοποιήστε ξανά τις στήλες
- Θέλετε να πολλαπλασιάσετε 34 x 6. Ξεκινάτε πολλαπλασιάζοντας τη στήλη μονάδων (4 x 6), αλλά δεν μπορείτε να έχετε 24 1s στη στήλη one.
-
Αποθηκεύστε 4 1s στη στήλη μονάδων. Μετακινήστε 2 10s στη στήλη των δεκάδων.
-
Πολλαπλασιάστε 6 x 3, που ισούται με 18. Προσθέστε το 2 που μετακινήσατε, το οποίο ισούται με 20.
Μέρος 6 από 6: Μαθηματικά βασικά-Αποκάλυψη προβλημάτων διαίρεσης

Βήμα 1. Σκεφτείτε τη διαίρεση σε αντίθεση με τον πολλαπλασιασμό
#* Εάν 4 x 4 = 16, τότε 16 /4 = 4.
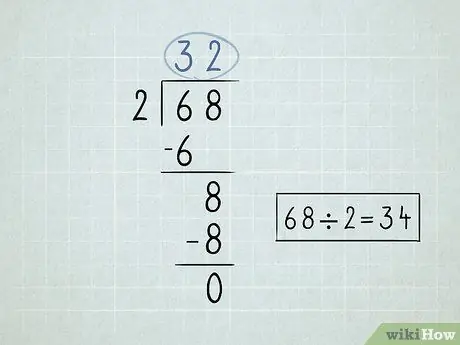
Βήμα 2. Καταγράψτε το πρόβλημα διαίρεσης
- Διαιρέστε τον αριθμό στα αριστερά του συμβόλου διαίρεσης ή διαιρέτη, με τον πρώτο αριθμό κάτω από το σύμβολο διαιρέτη. Δεδομένου ότι 6 /2 = 3, θα γράψετε τον αριθμό 3 πάνω από το σύμβολο διαίρεσης.
-
Πολλαπλασιάστε τον αριθμό πάνω από το σύμβολο διαίρεσης με τον διαιρέτη. Κατεβάστε το αποτέλεσμα στο κάτω μέρος του πρώτου αριθμού κάτω από το σύμβολο διαίρεσης. Αφού 3 x 2 = 6, τότε θα χαμηλώσετε τον αριθμό 6 προς τα κάτω.
- Αφαιρέστε τους 2 αριθμούς που έχετε γράψει. 6 - 6 = 0. Μπορείτε να αφήσετε το 0 κενό, επειδή γενικά δεν ξεκινάτε τους αριθμούς με το 0.
-
Κατεβάστε τον δεύτερο αριθμό που βρίσκεται κάτω από το σύμβολο διαίρεσης.
- Διαιρέστε τον αριθμό που κατεβάζετε με τον διαιρέτη. Σε αυτή την περίπτωση, 8 /2 = 4. Γράψτε τον αριθμό 4 πάνω από το σύμβολο διαίρεσης.
-
Πολλαπλασιάστε τον επάνω δεξιό αριθμό με τον διαιρέτη και μειώστε τον αριθμό. 4 x 2 = 8.
-
Αφαιρέστε αυτούς τους αριθμούς. Η τελική αφαίρεση επιστρέφει μηδέν, πράγμα που σημαίνει ότι έχετε λύσει το πρόβλημα. 68 x 2 = 34.

Βήμα 3. Υπολογίστε επίσης το υπόλοιπο
Μερικοί από τους διαιρέτες δεν χωρίζονται πλήρως σε άλλους αριθμούς. Εάν έχετε ολοκληρώσει την τελευταία αφαίρεση και δεν έχετε άλλους αριθμούς για να εξαγάγετε, τότε ο τελευταίος αριθμός είναι ο υπόλοιπος.






