- Συγγραφέας Jason Gerald [email protected].
- Public 2024-01-15 08:12.
- Τελευταία τροποποίηση 2025-01-23 12:15.
Στα στατιστικά, η λειτουργία είναι ο αριθμός που εμφανίζεται συχνότερα σε ένα σύνολο αριθμών ή δεδομένων. τα ίδια τα δεδομένα δεν έχουν πάντα μόνο μία λειτουργία, μπορεί να είναι δύο ή περισσότερες (έτσι ονομάζονται διτροπικά ή πολυτροπικά). Με άλλα λόγια, όλοι οι αριθμοί που εμφανίζονται συχνότερα σε ένα δεδομένα μπορούν να αναφέρονται ως τρόπος λειτουργίας. Για να μάθετε πώς μπορείτε να βρείτε τη λειτουργία, ακολουθήστε τα παρακάτω βήματα.
Βήμα
Μέθοδος 1 από 2: Εύρεση της λειτουργίας δεδομένων

Βήμα 1. Γράψτε τους αριθμούς στα δεδομένα
Η λειτουργία λαμβάνεται συνήθως από στατιστικά δεδομένα ή μια λίστα αριθμών. Έτσι χρειάζεστε δεδομένα για να βρείτε τη λειτουργία. Συνιστάται να καταγράψετε ή να καταγράψετε πρώτα τα δεδομένα, επειδή η εύρεση της λειτουργίας απλώς βλέποντας και αναλύοντάς την στο μυαλό σας είναι αρκετά δύσκολη, εκτός εάν τα δεδομένα είναι πολύ λίγα. Εάν χρησιμοποιείτε χαρτί και μολύβι ή στυλό, γράψτε πρώτα τα δεδομένα για να τα ταξινομήσετε αργότερα. Εάν χρησιμοποιείτε υπολογιστή, μπορείτε να χρησιμοποιήσετε ένα πρόγραμμα υπολογιστικών φύλλων για να τα ταξινομήσετε αυτόματα αργότερα.
Η διαδικασία εύρεσης της λειτουργίας ενός δεδομένων είναι ευκολότερο να κατανοηθεί εάν το ακολουθήσουμε από ένα παράδειγμα προβλήματος. Προς το παρόν, ας χρησιμοποιήσουμε αυτά τα δείγματα δεδομένων: {18, 21, 11, 21, 15, 19, 17, 21, 17} Το Στα επόμενα βήματα θα ανακαλύψουμε τη λειτουργία.

Βήμα 2. Ταξινόμηση των αριθμών από τον μικρότερο στον μεγαλύτερο
Η ταξινόμηση δεδομένων στην πραγματικότητα δεν μπορεί να γίνει. Αλλά αυτό το βήμα θα σας βοηθήσει πραγματικά να βρείτε τη λειτουργία, επειδή οι ίδιοι αριθμοί θα είναι ο ένας δίπλα στον άλλο, διευκολύνοντας τον υπολογισμό. Εάν το μέγεθος των δεδομένων σας είναι πολύ μεγάλο, αυτό το βήμα θα πρέπει να ληφθεί για να μειωθεί ο ρυθμός εμφάνισης που είναι επιρρεπής σε σφάλματα.
- Εάν χρησιμοποιείτε χαρτί και μολύβι ή στυλό, ξαναγράψτε τα δεδομένα που γράψατε νωρίτερα με τη σειρά. Ξεκινήστε βρίσκοντας τον μικρότερο αριθμό από τα δεδομένα. Εάν το βρείτε, γράψτε το σε μια νέα γραμμή και, στη συνέχεια, διαγράψτε τον αριθμό στην προηγούμενη λίστα δεδομένων. Βρείτε τον επόμενο μικρότερο αριθμό και κάντε το ίδιο πράγμα μέχρι να ταξινομήσετε όλους τους αριθμούς.
- Εάν χρησιμοποιείτε πρόγραμμα υπολογιστικών φύλλων στον υπολογιστή σας, μπορείτε να ταξινομήσετε τη λίστα αριθμών σε λίγα μόνο κλικ.
-
Στο παραπάνω παράδειγμά μας, τα ταξινομημένα δεδομένα είναι {11, 15, 17, 17, 18, 19, 21, 21, 21}.

Βήμα 3. Μετρήστε τον αριθμό των φορών που εμφανίζεται ένας αριθμός
Για μικρά δεδομένα, μπορείτε απλά να δείτε τα δεδομένα που έχουν ταξινομηθεί και, στη συνέχεια, να αναζητήσετε ποιος αριθμός είναι πιο ορατός εκεί. Εάν τα δεδομένα σας είναι μεγαλύτερα, τότε πρέπει να τα υπολογίσετε ένα προς ένα για να αποφύγετε σφάλματα.
- Εάν χρησιμοποιείτε χαρτί και μολύβι ή στυλό, για να αποφύγετε λανθασμένους υπολογισμούς, σημειώστε πόσες φορές εμφανίζεται κάθε αριθμός. Εάν χρησιμοποιείτε υπολογιστικό φύλλο σε υπολογιστή, μπορείτε επίσης να το καταγράψετε σε άλλη στήλη ή εάν γνωρίζετε, μπορείτε να χρησιμοποιήσετε τους τύπους που παρέχονται στο πρόγραμμα.
- Στο παράδειγμα του προβλήματος, δηλαδή ({11, 15, 17, 17, 18, 19, 21, 21, 21}), ο αριθμός 11 εμφανίζεται μία φορά, 15 εμφανίζεται μία φορά, 17 εμφανίζεται δύο φορές, 18 εμφανίζεται μία φορά, 19 εμφανίζεται μία φορά, και 21 εμφανίζεται τρεις φορές Το Από εκεί, είναι σαφές ότι το 21 είναι ο αριθμός που εμφανίζεται συχνότερα.

Βήμα 4. Ο αριθμός που εμφανίζεται συχνότερα είναι η λειτουργία των δεδομένων
Αφού σημειώσετε πόσες φορές εμφανίζεται ο καθένας από τους ίδιους αριθμούς, θα πρέπει να το γνωρίζετε ήδη ποιος αριθμός εμφανίζεται περισσότερο, πράγμα που σημαίνει τη λειτουργία δεδομένων Το Να θυμάστε ότι είναι πιθανό τα δεδομένα να έχουν περισσότερες από μία λειτουργίες Το Εάν ένα δεδομένο έχει δύο τρόπους λειτουργίας, τότε τα δεδομένα μπορούν να ονομαστούν διτροπικά, ενώ αν έχουν τρεις λειτουργίες, ονομάζονται τριμερή και ούτω καθεξής.
- Στο πρόβλημα του παραδείγματος, η λειτουργία είναι 21 επειδή εμφανίζεται συχνότερα.
- Εάν υπάρχει άλλος αριθμός που εμφανίζεται επίσης τρεις φορές, τότε 21 και αυτός είναι ο τρόπος λειτουργίας.

Βήμα 5. Διαφοροποιήστε τη λειτουργία των δεδομένων με τη μέση τιμή (μέση τιμή) και τη διάμεσο
Οι τρεις στατιστικές έννοιες συζητούνται συνήθως σε μία συζήτηση. Επειδή έχουν παρόμοια ονόματα και μερικές φορές έχουν την ίδια αξία, πολλοί άνθρωποι δυσκολεύονται να τα ξεχωρίσουν. Ωστόσο, παρόλο που τα δεδομένα μπορεί να έχουν την ίδια λειτουργία, διάμεσο ή μέσο όρο, λάβετε υπόψη ότι είναι διαφορετικά και είναι ανεξάρτητα. Διαβάστε την εξήγηση παρακάτω.
-
Ο μέσος όρος που σημαίνει τον μέσο όρο είναι το άθροισμα των τιμών δεδομένων διαιρούμενο με τον αριθμό των δεδομένων. Για παράδειγμα, στο παράδειγμα του προβλήματος ({11, 15, 17, 17, 18, 19, 21, 21, 21}), τα συνολικά δεδομένα είναι 11 + 15 + 17 + 17 + 18 + 19 + 21 + 21 + 21 = 160. Και επειδή υπάρχουν 9 τιμές στα δεδομένα, τότε 160/9 = 17.78.

Βρείτε τη λειτουργία ενός συνόλου αριθμών Βήμα 5Bullet1 -
Η διάμεσος είναι η μεσαία τιμή μετά την ταξινόμηση των δεδομένων και διαχωρίζει τις μικρές και μεγάλες τιμές από τα δεδομένα. Στο παράδειγμα του προβλήματος, ({11, 15, 17, 17, 18, 19, 21, 21, 21}), ο διάμεσος είναι
Βήμα 18. επειδή ο αριθμός είναι στη μέση και υπάρχουν τέσσερις αριθμοί υψηλότεροι και τέσσερις αριθμοί χαμηλότεροι από 18 στα δεδομένα. Εάν τα δεδομένα είναι ζυγός αριθμός, ο μέσος όρος λαμβάνεται υπολογίζοντας το άθροισμα των δύο αριθμών στη μέση και στη συνέχεια διαιρώντας με δύο.

Βρείτε τη λειτουργία ενός συνόλου αριθμών Βήμα 5Bullet2
Μέθοδος 2 από 2: Εύρεση της λειτουργίας σε ένα ειδικό πρόβλημα

Βήμα 1. Τα δεδομένα δεν έχουν λειτουργία εάν όλοι οι αριθμοί στα δεδομένα έχουν τον ίδιο αριθμό εμφανίσεων
Για παράδειγμα, εάν όλοι οι αριθμοί εμφανίζονται μόνο μία φορά, τα δεδομένα χωρίς λειτουργία γιατί κανένας αριθμός δεν εμφανίζεται συχνότερα από τον άλλο. Το ίδιο ισχύει εάν όλοι οι αριθμοί εμφανίζονται δύο φορές ή περισσότεροι.
Εάν αλλάξουμε τα δεδομένα στο παραπάνω πρόβλημα σε {11, 15, 17, 18, 19, 21}, που σημαίνει ότι όλοι οι αριθμοί εμφανίζονται μία φορά, τότε τα δεδομένα δεν έχουν λειτουργία, καθώς και εάν τα δεδομένα αλλάξουν σε {11, 11, 15, 15, 17, 17, 18, 18, 19, 19, 21, 21}

Βήμα 2. Τα μη αριθμητικά δεδομένα μπορούν να αναζητηθούν για τη λειτουργία τους, όπως τα αριθμητικά δεδομένα
Συνήθως τα δεδομένα υπάρχουν σε ποσοτική ή αριθμητική μορφή, επομένως μπορούν να υποβληθούν σε επεξεργασία με πολλές μεθόδους. Ωστόσο, μερικές φορές υπάρχουν πράγματα που δεν έχουν τη μορφή αριθμών. Ωστόσο, αυτός ο τρόπος δεδομένων μπορεί ακόμα να αναζητηθεί απλά αναζητώντας τα δεδομένα (τα οποία μπορεί να έχουν τη μορφή δηλώσεων) που εμφανίζονται συχνότερα. Αλλά δεν μπορείτε να βρείτε τον μέσο ή τον μέσο για μη αριθμητικά δεδομένα.
- Για παράδειγμα, ας υποθέσουμε ότι πραγματοποιείτε μια βιολογική έρευνα, η οποία είναι να μάθετε ποια είδη δέντρων αναπτύσσονται στην περιοχή σας. Τα δεδομένα που λαμβάνετε είναι {Fire, Mango, Spruce, Palm, Spruce, Fir, Mango, Mango, Palm, Fir}. Αυτά τα δεδομένα ονομάζονται ονομαστικά δεδομένα επειδή κάθε τιμή δεδομένων διακρίνεται από ένα όνομα. Για αυτό το παράδειγμα, η λειτουργία είναι έλατο επειδή εμφανίζεται συχνότερα (πέντε φορές).
- Αν κοιτάξετε το παράδειγμα, δεν υπάρχει τρόπος να υπολογίσετε τον μέσο όρο ή τον διάμεσο.
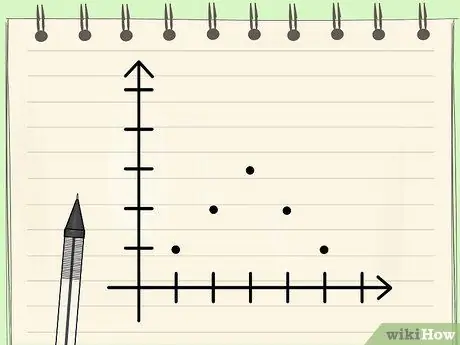
Βήμα 3. Γνωρίστε ότι για μια συμμετρική μονοτροπική κατανομή δεδομένων, ο τρόπος, ο διάμεσος και ο μέσος όρος των δεδομένων θα είναι οι ίδιοι
Όπως αναφέρθηκε προηγουμένως, θα υπάρξουν στιγμές που ο μέσος όρος, ο διάμεσος και ο τρόπος ενός συνόλου δεδομένων θα είναι οι ίδιοι. Μία από τις προϋποθέσεις είναι εάν τα δεδομένα έχουν αυστηρά συμμετρική κατανομή τιμών (οι οποίες αν σχεδιαστούν σε γραφική μορφή θα σχηματίσουν μια καμπύλη σε σχήμα καμπάνας Gauss). Επειδή η κατανομή είναι συμμετρική, ο τρόπος δεδομένων όπως αυτό είναι αυτόματα τα δεδομένα που βρίσκονται στη μέση, επειδή πρέπει να είναι τα δεδομένα που εμφανίζονται συχνότερα και επειδή είναι η μεσαία τιμή, σημαίνει ότι ο αριθμός είναι και ο διάμεσος Το Και αν κάνετε τα μαθηματικά, ο μέσος όρος θα δώσει τον ίδιο αριθμό.
- Για παράδειγμα, από τα δεδομένα {1, 2, 2, 3, 3, 3, 4, 4, 5}, αν σχεδιάσετε το γράφημα, θα λάβετε ένα γράφημα παραβολής. Η λειτουργία δεδομένων είναι 3 επειδή εμφανίζεται συχνότερα, ο διάμεσος είναι 3 επειδή ο αριθμός είναι στη μέση, και ο μέσος όρος είναι 1 + 2 + 2 + 3 + 3 + 3 + 4 + 4 + 5 = 27/9 = 3.
- Περιπτώσεις όπως αυτή έχουν εξαιρέσεις, δηλαδή όταν αυτά τα συμμετρικά δεδομένα έχουν περισσότερες από μία λειτουργίες. Εάν συμβαίνει αυτό, επειδή ο μέσος όρος και ο διάμεσος δεν μπορούν να είναι περισσότερες από μία τιμές, τότε ο τρόπος λειτουργίας δεν θα είναι ο ίδιος με τον μέσο και τον διάμεσο.
Συμβουλές
- Τα δεδομένα μπορούν να έχουν περισσότερες από μία λειτουργίες
- Εάν ο αριθμός εμφανίσεων όλων των αριθμών σε ένα δεδομένα είναι ο ίδιος, τότε η λειτουργία δεδομένων δεν υπάρχει.






