Το IQR είναι το εύρος των τεταρτημορίων ή το εύρος τεταρτημόριο ρίζας ενός συνόλου δεδομένων. Το IQR χρησιμοποιείται στη στατιστική ανάλυση για να βοηθήσει στην εξαγωγή συμπερασμάτων σχετικά με ένα σύνολο δεδομένων. Το IQR χρησιμοποιείται συχνότερα από το εύρος επειδή το IQR δεν περιλαμβάνει τα εξόχως απόκεντρα δεδομένα. Συνεχίστε να διαβάζετε για να μάθετε πώς μπορείτε να βρείτε το IQR!
Βήμα
Μέθοδος 1 από 3: Κατανόηση του IQR
Βήμα 1. Κατανοήστε τον τρόπο χρήσης του IQR
Βασικά, το IQR είναι ένας τρόπος κατανόησης της διάδοσης ενός συνόλου αριθμών. Το εύρος τεταρτημόριο ρίζας ορίζεται ως η διαφορά μεταξύ του ανώτερου τεταρτημορίου (25% κορυφή) και του κάτω τεταρτημορίου (25% χαμηλότερο) του συνόλου δεδομένων.
Υπόδειξη:
Το κατώτερο τεταρτημόριο γράφεται συνήθως ως Q1 και το άνω τεταρτημόριο γράφεται ως Q3 - το οποίο τεχνικά καθιστά το μέσο σημείο των δεδομένων Q2 και το υψηλότερο σημείο Q4.
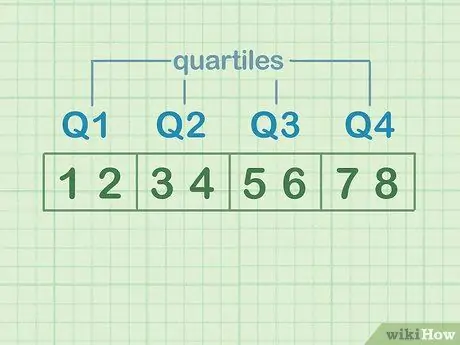
Βήμα 2. Κατανοήστε τα τεταρτημόρια
Για να απεικονίσετε τεταρτημόρια, διαιρέστε το σύνολο των αριθμών σε τέσσερα ίσα μέρη. Κάθε ένα από αυτά τα μέρη είναι ένα "τεταρτημόριο". Ας υποθέσουμε ότι τα σύνολα δεδομένων είναι: 1, 2, 3, 4, 5, 6, 7, 8.
- 1 και 2 είναι το πρώτο τεταρτημόριο ή Q1
- 3 και 4 είναι το δεύτερο τεταρτημόριο ή Q2
- 5 και 6 είναι το τρίτο τεταρτημόριο ή Q3
- Τα 7 και 8 είναι το τέταρτο τεταρτημόριο ή Q4
Βήμα 3. Μάθετε τον τύπο
Για να βρείτε τη διαφορά μεταξύ του άνω και του κάτω τεταρτημορίου, πρέπει να αφαιρέσετε το 75ο εκατοστημόριο από το 25ο εκατοστημόριο.
Ο τύπος είναι γραμμένος: Q3 - Q1 = IQR
Μέθοδος 2 από 3: Συγκέντρωση του συνόλου δεδομένων
Βήμα 1. Συλλέξτε τα δεδομένα σας
Εάν μελετάτε IQR στην τάξη και στις δοκιμές, μπορεί να σας δοθεί ένα σύνολο δεδομένων που έχουν ήδη προετοιμαστεί, για παράδειγμα 1, 4, 5, 7, 10. Αυτό είναι το σύνολο δεδομένων σας - οι αριθμοί με τους οποίους θα εργαστείτε. Ωστόσο, μπορείτε να δημιουργήσετε τους δικούς σας αριθμούς από ερωτήσεις πίνακα ή προβλήματα ιστορίας.
Βεβαιωθείτε ότι κάθε αριθμός αντιπροσωπεύει το ίδιο πράγμα:
για παράδειγμα, ο αριθμός των αυγών σε κάθε φωλιά ενός καθορισμένου πληθυσμού πτηνών ή ο αριθμός των θέσεων στάθμευσης που βρίσκονται σε κάθε σπίτι σε ένα καθορισμένο συγκρότημα.
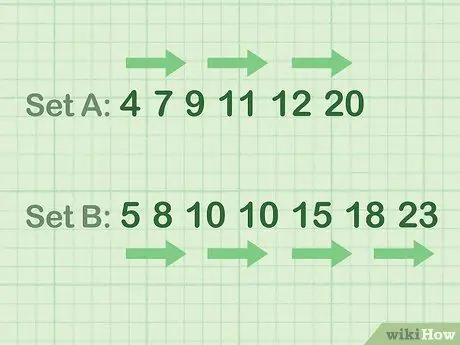
Βήμα 2. Ταξινομήστε τα δεδομένα σας με αύξουσα σειρά
Με άλλα λόγια: τακτοποιήστε τους αριθμούς από τον μικρότερο στον μεγαλύτερο. Χρησιμοποιήστε τις συμβουλές από τα ακόλουθα παραδείγματα.
- Παράδειγμα δεδομένων ζυγού αριθμού (Σύνολο Α): 4 7 9 11 12 20
- Παράδειγμα δεδομένων περιττού αριθμού (σύνολο Β): 5 8 10 10 15 18 23 23
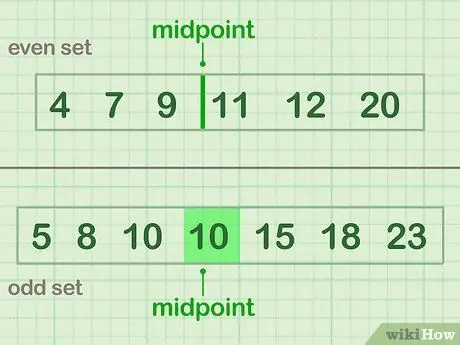
Βήμα 3. Χωρίστε τα δεδομένα στα δύο
Για να χωρίσετε στο μισό, βρείτε το μέσο των δεδομένων σας: τον αριθμό ή τους αριθμούς που βρίσκονται στο κέντρο του συνόλου δεδομένων. Εάν έχετε έναν περιττό αριθμό δεδομένων, επιλέξτε τον αριθμό που βρίσκεται ακριβώς στη μέση. Εάν έχετε ζυγό αριθμό δεδομένων, το μεσαίο σημείο βρίσκεται μεταξύ των δύο πιο μεσαίων αριθμών.
- Ένα άρτιο παράδειγμα (Σύνολο Α) το οποίο έχει ένα μεσαίο σημείο μεταξύ 9 και 11: 4 7 9 | 11 12 20
- Ένα περίεργο παράδειγμα (Σύνολο Β) που έχει ένα μέσο σημείο τιμής (10): 5 8 10 (10) 15 18 23
Μέθοδος 3 από 3: Υπολογισμός IQR
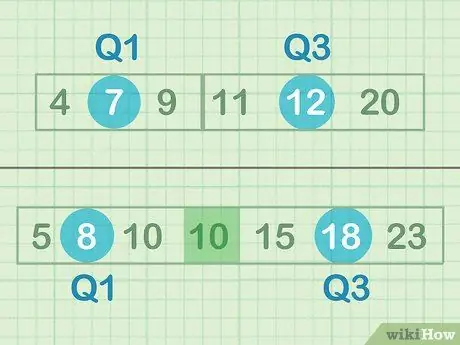
Βήμα 1. Βρείτε τη διάμεσο του κάτω και άνω μισού των δεδομένων σας
Ο διάμεσος είναι το "μεσαίο σημείο" ή αριθμός που βρίσκεται στη μέση ενός συνόλου αριθμών. Σε αυτή την περίπτωση, δεν αναζητάτε το μεσαίο σημείο όλων των αριθμών, αλλά αναζητάτε το σχετικό μεσαίο σημείο των άνω και κάτω υποσυνόλων δεδομένων. Εάν έχετε έναν μονό αριθμό δεδομένων, μην συμπεριλάβετε τον μεσαίο αριθμό - για παράδειγμα, στο Σετ Β, δεν χρειάζεται να συμπεριλάβετε ένα μόνο 10.
-
Ακόμη και παράδειγμα (σύνολο Α):
- Μέσος όρος του κάτω μισού των δεδομένων = 7 (Q1)
- Μέσος όρος του άνω μισού των δεδομένων = 12 (Q3)
-
Παράξενο παράδειγμα (σύνολο Β):
- Μέσος όρος του κάτω μισού των δεδομένων = 8 (Q1)
- Μέσος όρος του άνω μισού των δεδομένων = 18 (Q3)
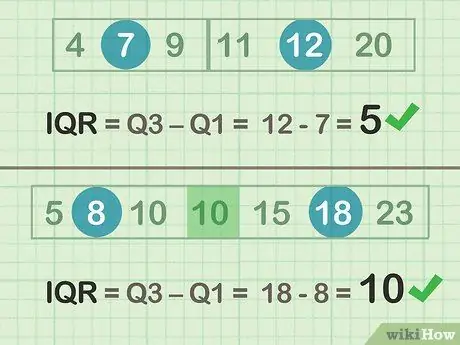
Βήμα 2. Αφαιρέστε το Q3-Q1 για να προσδιορίσετε το IQR
Τώρα ξέρετε πόσοι αριθμοί πέφτουν μεταξύ του 25ου και του 75ου εκατοστημορίου. Μπορείτε να χρησιμοποιήσετε αυτόν τον αριθμό για να κατανοήσετε την εξάπλωση των δεδομένων. Για παράδειγμα, εάν μια δοκιμή έχει μέγιστη βαθμολογία 100 και το IQR της βαθμολογίας είναι 5, μπορείτε να υποθέσετε ότι οι περισσότεροι άνθρωποι που κάνουν το τεστ έχουν σχεδόν την ίδια κατανόηση επειδή το εύρος των υψηλών και χαμηλών επιπέδων δεν είναι πολύ μεγάλο. Ωστόσο, εάν το IQR μιας βαθμολογίας δοκιμής είναι 30, μπορεί να αρχίσετε να αναρωτιέστε γιατί κάποιοι σκοράρουν τόσο υψηλά και άλλοι τόσο χαμηλά.
- Παράδειγμα (σύνολο Α): 12 -7 = 5
- Μονό παράδειγμα (σύνολο Β): 18 - 8 = 10
Συμβουλές
Είναι σημαντικό να μάθετε να το κάνετε μόνοι σας. Ωστόσο, υπάρχουν αρκετοί ηλεκτρονικοί υπολογιστές IQR που μπορείτε να χρησιμοποιήσετε για να ελέγξετε την εργασία σας. Μην βασίζεστε πολύ στις εφαρμογές αριθμομηχανής αν το μάθετε αυτό στην τάξη! Εάν σας ζητηθεί να αναζητήσετε το IQR σε μια δοκιμή, θα πρέπει να ξέρετε πώς να το βρείτε χειροκίνητα
Σχετικό WikiHow
- Πώς να εντοπίσετε τις υπερβολικές τιμές
- Πώς να υπολογίσετε το εύρος ενός συνόλου δεδομένων
- Πώς να φτιάξετε ένα διάγραμμα κουτιού και σκηνής
