- Συγγραφέας Jason Gerald gerald@how-what-advice.com.
- Public 2024-01-16 19:20.
- Τελευταία τροποποίηση 2025-01-23 12:15.
Η ταχύτητα είναι ένας υπολογισμός του πόσο γρήγορα κινείται κάτι ταυτόχρονα. Αν έχετε κοιτάξει ποτέ το ταχύμετρο ενός κινούμενου αυτοκινήτου, θα δείτε την ταχύτητα να μετράει - όσο πιο μακριά κινείται η βελόνα, τόσο μεγαλύτερη είναι η ταχύτητα του οχήματος. Υπάρχουν διάφοροι τρόποι υπολογισμού της ταχύτητας, ανάλογα με τον τύπο των πληροφοριών που έχετε. Γενικά, ο τύπος ταχύτητα = απόσταση/χρόνος (ή k = j/w) είναι ο ευκολότερος τρόπος υπολογισμού της ταχύτητας.
Βήμα
Μέθοδος 1 από 3: Χρήση τυποποιημένων τύπων υπολογισμού ταχύτητας

Βήμα 1. Βρείτε την απόσταση που έχει διανύσει ένα αντικείμενο
Η βασική φόρμουλα που χρησιμοποιούν οι περισσότεροι για να βρουν την ταχύτητα κάτι είναι πολύ εύκολη στη χρήση. Πρώτα απ 'όλα, πρέπει να γνωρίζετε "πόση απόσταση έχει διανύσει το μετρημένο αντικείμενο". Με άλλα λόγια, ποια είναι η απόσταση μεταξύ του σημείου εκκίνησης και του τελικού σημείου του αντικειμένου;
Αυτός ο τύπος είναι ευκολότερο να κατανοηθεί μέσω ενός παραδείγματος. Ας πούμε ότι ταξιδεύουμε με αυτοκίνητο σε παιδική χαρά για «161 χιλιόμετρα». Σε λίγα βήματα, μπορούμε να χρησιμοποιήσουμε αυτές τις πληροφορίες για να ολοκληρώσουμε τον υπολογισμό του τύπου

Βήμα 2. Βρείτε το χρόνο που χρειάζεται το αντικείμενο για να διανύσει αυτήν την απόσταση
Οι επόμενες πληροφορίες που χρειάζεστε είναι πόσος χρόνος χρειάζεται το αντικείμενο για να φτάσει σε μια ορισμένη απόσταση. Με άλλα λόγια, πόσος χρόνος χρειάζεται για να μετακινηθεί το αντικείμενο από το σημείο εκκίνησης στο τελικό σημείο;
Σε αυτό το παράδειγμα, ας πούμε ότι το αντικείμενο παίρνει περίπου. δύο ώρες για να φτάσετε στον προορισμό.

Βήμα 3. Χωρίστε την απόσταση με το χρόνο που απαιτείται για να βρείτε την ταχύτητα του αντικειμένου
Χρειάζεστε μόνο αυτές τις δύο πληροφορίες για να γνωρίζετε την ταχύτητα του αντικειμένου. Η απόσταση στο χρόνο είναι ίση με την ταχύτητα του αντικειμένου.
Σε αυτό το παράδειγμα, 161 χιλιόμετρα/2 ώρες = 80,5 χιλιόμετρα/ώρα.

Βήμα 4. Μην ξεχνάτε τη μονάδα που χρησιμοποιείται
Είναι πολύ σημαντικό να χρησιμοποιήσετε τις σωστές μονάδες στην απάντησή σας (όπως χιλιόμετρα την ώρα κ.λπ.) Χωρίς αυτές τις μονάδες, είναι πολύ δύσκολο για τους ανθρώπους να καταλάβουν το νόημα της απάντησής σας. Μπορείτε επίσης να χάσετε πόντους εάν χρησιμοποιήσετε λάθος μονάδα όταν κάνετε εργασίες από το σχολείο.
Η μονάδα ταχύτητας είναι μονάδα απόστασης σε μονάδα χρόνου Το Για παράδειγμα, δεδομένου ότι μετράμε την απόσταση σε χιλιόμετρα και τον χρόνο σε ώρες, οι μονάδες που χρησιμοποιούνται είναι χιλιόμετρα/ώρα (ή χιλιόμετρα την ώρα).
Μέθοδος 2 από 3: Επίλυση δυσκολότερων υπολογισμών

Βήμα 1. Βρείτε αρκετές διαφορετικές μεταβλητές για να λύσετε το πρόβλημα της απόστασης και του χρόνου
Μόλις κατανοήσετε τον βασικό τύπο για την ταχύτητα, μπορείτε να τον χρησιμοποιήσετε για να εκτελέσετε άλλους υπολογισμούς εκτός από την ταχύτητα. Για παράδειγμα, εάν στην αρχή γνωρίζετε μόνο την ταχύτητα του αντικειμένου και μιας άλλης μεταβλητής, μπορείτε να αναδιατάξετε τον παραπάνω τύπο για να βρείτε τις άγνωστες πληροφορίες.
-
Για παράδειγμα, ας πούμε ότι γνωρίζουμε ότι ένα τρένο ταξιδεύει με 20 χιλιόμετρα την ώρα για τέσσερις ώρες, αλλά δεν ξέρουμε πόσο μακριά έχει διανύσει. Για να μάθετε, μπορούμε να αναδιατάξουμε τον τύπο με τον ακόλουθο τρόπο:
-
- ταχύτητα = απόσταση/χρόνος
- ταχύτητα × χρόνος = (απόσταση/χρόνος) × χρόνος
- ταχύτητα × χρόνος = απόσταση
- 20 χλμ/ώρα × 4 ώρες = απόσταση = 80 χιλιόμετρα
-

Βήμα 2. Μετατρέψτε τις μονάδες που χρησιμοποιείτε όπως απαιτείται
Μερικές φορές, μπορείτε να υπολογίσετε την ταχύτητα χρησιμοποιώντας μια συγκεκριμένη μονάδα, αλλά πρέπει να τη μετατρέψετε σε άλλη μονάδα. Σε αυτήν την περίπτωση, πρέπει να χρησιμοποιήσετε έναν συντελεστή μετατροπής για να λάβετε την απάντηση σύμφωνα με τις σωστές μονάδες. Για να γίνει αυτό, απλά γράψτε τη σχέση μεταξύ των μονάδων σε μορφή κλάσματος και πολλαπλασιάστε. Όταν πολλαπλασιάζετε, αντιστρέψτε το κλάσμα όπως απαιτείται για να αφαιρέσετε ανεπιθύμητες μονάδες. Αυτή η μέθοδος είναι πολύ πιο εύκολη από ό, τι ακούγεται!
-
Για παράδειγμα, ας πούμε ότι στο παραπάνω πρόβλημα, χρειαζόμαστε την απάντηση σε μίλια αντί σε χιλιόμετρα. Ένα μίλι ισούται με περίπου 1,6 χιλιόμετρα. Έτσι, μπορούμε να κάνουμε τη μετατροπή ως εξής:
-
- 80 χιλιόμετρα × 1 μίλι/1,6 χιλιόμετρα = 50 μίλια
-
- Θυμηθείτε, επειδή τα χιλιόμετρα εμφανίζονται στο κάτω μέρος του κλάσματος, αφαιρεί χιλιόμετρα από την προηγούμενη απάντηση, οπότε το τελικό αποτέλεσμα χρησιμοποιεί μίλια.
- Αυτός ο ιστότοπος παρέχει δυνατότητες μετατροπής για τις περισσότερες από τις κοινώς χρησιμοποιούμενες μονάδες.

Βήμα 3. Αντικαταστήστε τη μεταβλητή "απόσταση" με τον τύπο απόστασης, όπως απαιτείται
Τα αντικείμενα δεν κινούνται πάντα σε μια ευθεία, ομαλή διαδρομή. Εάν αυτό ισχύει, ενδέχεται να μην μπορείτε να εισαγάγετε απλά μια αριθμητική τιμή ως μονάδα απόστασης στον τυπικό τύπο ταχύτητας. Ωστόσο, ίσως χρειαστεί να αντικαταστήσετε το γράμμα j στον τύπο k = j/w με έναν τύπο που μοιάζει με την απόσταση που διανύει το αντικείμενο.
-
Για παράδειγμα, ας πούμε ότι ένα αεροπλάνο περιστρέφεται στον αέρα σε απόσταση 20 μιλίων 5 φορές. Το αεροπλάνο ολοκλήρωσε τον γύρο σε μισή ώρα. Σε αυτό το παράδειγμα, πρέπει ακόμη να βρούμε τη συνολική απόσταση που διανύει το αεροπλάνο προτού μπορέσουμε να προσδιορίσουμε την ταχύτητά του. Μπορούμε να χρησιμοποιήσουμε τον τύπο για τον υπολογισμό της απόστασης γύρω από έναν κύκλο (απόσταση γύρω από αυτόν) αντί για j σε αυτόν τον τύπο. Αυτός ο τύπος είναι περιφέρεια = 2πr όπου r = ακτίνα κύκλου. Δείτε πώς μπορείτε να το λύσετε:
-
- k = (2 × × r)/w
- k = (2 × × 10) /0.5
- k = 62.83/0.5 = 125,66 μίλια/ώρα
-

Βήμα 4. Κατανοήστε ότι k = j/w δίνει τη μέση ταχύτητα
Ο εύκολος και απλός τύπος που χρησιμοποιούμε για να βρούμε την ταχύτητα έχει ένα μειονέκτημα. Η τιμή που προκύπτει είναι τεχνικά η μέση ταχύτητα. Αυτό σημαίνει ότι ο τύπος υποθέτει ότι το αντικείμενο που μετράτε χρησιμοποιεί την ίδια ταχύτητα καθώς κινείται. Όπως θα δούμε παρακάτω, η εύρεση της ταχύτητας ενός αντικειμένου σε μία μόνο στιγμή θα είναι πολύ πιο δύσκολη.
Για να καταδείξετε αυτή τη διαφορά, φανταστείτε την τελευταία φορά που ταξιδέψατε με αυτοκίνητο. Είναι απίθανο να ταξιδεύετε με την ίδια ταχύτητα που ταξιδεύετε. Ωστόσο, συνήθως ξεκινάτε το ταξίδι σας με χαμηλή ταχύτητα και σταδιακά αυξάνετε την ταχύτητά σας στην πορεία, σταματώντας λόγω κόκκινων φανών, μποτιλιάρισμα κ.λπ. Εάν χρησιμοποιείτε τον τυπικό τύπο ταχύτητας για να βρείτε ταχύτητα κατά τη διάρκεια του ταξιδιού, δεν μπορούν να εντοπιστούν αλλαγές σε αυτήν την ταχύτητα. Ωστόσο, θα λάβετε μια απάντηση που δείχνει τη μέση ταχύτητα όλων των διαφορών ταχύτητας που ταξιδεύετε
Μέθοδος 3 από 3: Υπολογισμός στιγμιαίας ταχύτητας
Σημείωση:
Αυτή η ενότητα χρησιμοποιεί τεχνικές που είναι λιγότερο οικείες σε άτομα που δεν έχουν σπουδάσει ποτέ λογισμούς. Διαβάστε τα άρθρα μας σχετικά με τον λογισμό για βοήθεια.
Βήμα 1. Κατανοήστε ότι η ταχύτητα ορίζεται ως ο ρυθμός επιτάχυνσης
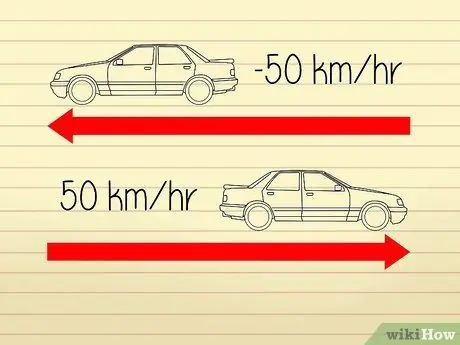
Οι υπολογισμοί ταχύτητας υψηλού επιπέδου είναι αρκετά μπερδεμένοι επειδή μαθηματικοί και επιστήμονες χρησιμοποιούν διαφορετικούς ορισμούς για να περιγράψουν την "ταχύτητα" και την "επιτάχυνση". Η επιτάχυνση έχει δύο συστατικά: έναν "ρυθμό" και μια "κατεύθυνση". Ο ρυθμός είναι ίσος με την ταχύτητα του αντικειμένου. Μια αλλαγή κατεύθυνσης θα προκαλέσει αλλαγή στην επιτάχυνση, αλλά όχι αλλαγή ταχύτητας.
- Για παράδειγμα, ας πούμε ότι δύο αυτοκίνητα κινούνται σε αντίθετες κατευθύνσεις. Τα ταχύμετρα και στα δύο αυτοκίνητα εμφανίζουν έναν αριθμό 50 km/h, οπότε και τα δύο ταξιδεύουν με την ίδια ταχύτητα. Ωστόσο, δεδομένου ότι τα αυτοκίνητα απομακρύνονται το ένα από το άλλο, μπορούμε να πούμε ότι το ένα από τα αυτοκίνητα έχει "επιτάχυνση" -50 km/h ενώ το άλλο "επιτάχυνση" 50 km/h.
- Ακριβώς όπως οι στιγμιαίοι υπολογισμοί ταχύτητας, μπορείτε επίσης να εκτελέσετε υπολογισμούς στιγμιαίας επιτάχυνσης.

Βήμα 2. Χρησιμοποιήστε απόλυτες τιμές για να μετρήσετε την αρνητική επιτάχυνση
Ένα αντικείμενο μπορεί να έχει αρνητικό ρυθμό επιτάχυνσης (εάν κινείται σε αρνητική κατεύθυνση σε σχέση με άλλο αντικείμενο). Ωστόσο, δεν υπάρχει αρνητική ταχύτητα. Έτσι, σε αυτή την περίπτωση, η απόλυτη τιμή του ρυθμού δείχνει την ταχύτητα του αντικειμένου.
Για το λόγο αυτό, στο παραπάνω πρόβλημα, και τα δύο αυτοκίνητα έχουν ταχύτητα 50 χλμ./Ώρα.
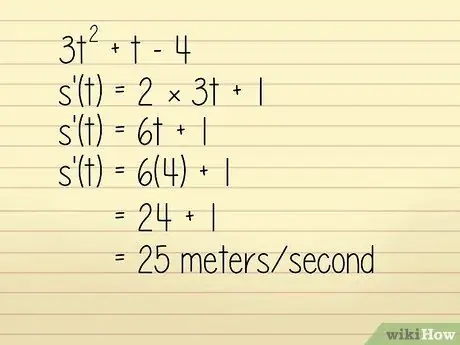
Βήμα 3. Πάρτε το παράγωγο της θέσης της συνάρτησης
Εάν έχετε μια συνάρτηση k (w) που δείχνει τη θέση ενός αντικειμένου χωρίς να χρειάζεται να υπολογίσετε το χρόνο, το παράγωγο του k (w) θα δείξει την επιτάχυνση χωρίς να απαιτείται χρονισμός. Απλώς συνδέστε την τιμή χρόνου σε αυτόν τον τύπο, έτσι ώστε η μεταβλητή w (ή οποιαδήποτε άλλη χρονική τιμή χρησιμοποιείται) να επιταχυνθεί σύμφωνα με αυτόν τον χρόνο. Από εδώ, μπορείτε εύκολα να βρείτε την ταχύτητα του αντικειμένου.
-
Για παράδειγμα, ας πούμε ότι η θέση ενός αντικειμένου σε ένα μέτρο περιγράφεται στην εξίσωση 3q2 + w - 4 όπου w = χρόνος σε δευτερόλεπτα. Θέλουμε να γνωρίζουμε την ταχύτητα του αντικειμένου σε w = 4 δευτερόλεπτα. Σε αυτήν την περίπτωση, μπορείτε να το λύσετε με:
-
- 3w2 +w - 4
- k '(w) = 2 × 3w + 1
- k '(w) = 6w + 1
-
-
Τώρα, εισάγουμε w = 4:
-
- k '(w) = 6 (4) + 1 = 24 + 1 = 25 μέτρα/δευτερόλεπτο Το Τεχνικά αυτός είναι ένας υπολογισμός της επιτάχυνσης, αλλά επειδή είναι θετικός και η κατεύθυνση δεν αναφέρεται στην ερώτηση, μπορούμε να τον χρησιμοποιήσουμε για να βρούμε ταχύτητα.
-

Βήμα 4. Πάρτε την ολοκληρωμένη συνάρτηση επιτάχυνσης
Η επιτάχυνση είναι ένας τρόπος μέτρησης της αλλαγής στην επιτάχυνση ενός αντικειμένου με την πάροδο του χρόνου. Αυτό το θέμα είναι πολύ περίπλοκο για να εξηγηθεί πλήρως σε αυτό το άρθρο. Ωστόσο, είναι χρήσιμο να σημειωθεί ότι όταν έχετε μια συνάρτηση a (w) που αντιπροσωπεύει την επιτάχυνση σε σχέση με το χρόνο, το ολοκλήρωμα του a (w) θα επιστρέψει το αποτέλεσμα της επιτάχυνσης με βάση αυτόν τον χρόνο. Θυμηθείτε, είναι πολύ χρήσιμο να γνωρίζετε την αρχική επιτάχυνση ενός αντικειμένου, ώστε να μπορείτε να ορίσετε τη σταθερά αυτού του αποτελέσματος από ένα άπειρο ολοκλήρωμα.
-
Για παράδειγμα, ας πούμε ότι ένα αντικείμενο έχει σταθερή επιτάχυνση (σε m/s2 ως αποτέλεσμα του (w) = -30. Πείτε επίσης ότι το αντικείμενο έχει αρχική επιτάχυνση 10 m/s. Πρέπει να βρούμε την ταχύτητα στο w = 12 δευτερόλεπτα. Σε αυτήν την περίπτωση, μπορούμε να το λύσουμε με:
-
- α (w) = -30
- p (w) = a (w) dw = -30dw = -30w + C
-
-
Για να βρούμε το C, θα λύσουμε το p (w) για το w = 0. Να θυμάστε ότι η αρχική επιτάχυνση του αντικειμένου είναι 10 m/s.
-
- p (0) = 10 = -30 (0) + C
- 10 = C, άρα p (w) = -30w + 10
-
-
Τώρα, μπορούμε να εισάγουμε w = 12 δευτερόλεπτα.
-
- p (12) = -30 (12) + 10 = -360 + 10 = -350. Δεδομένου ότι η ταχύτητα είναι απόλυτη τιμή επιτάχυνσης, η ταχύτητα του αντικειμένου είναι 350 μέτρα/δευτερόλεπτο.
-
Συμβουλές
- Η πρακτική κάνει υπέροχα! Προσπαθήστε να δημιουργήσετε τη δική σας ερώτηση αντικαθιστώντας τους αριθμούς στο παραπάνω πρόβλημα παραδείγματος.
- Αν ψάχνετε για έναν γρήγορο τρόπο εξάσκησης υπολογισμού για καλύτερη ταχύτητα υπολογισμού, χρησιμοποιήστε την ηλεκτρονική αριθμομηχανή παραγώγων εδώ και την ηλεκτρονική ενσωματωμένη αριθμομηχανή εδώ.






