Εφόσον γνωρίζετε το μέτρο των άλλων δύο γωνιών, η εύρεση της τρίτης γωνίας ενός τριγώνου είναι εύκολη. Απλώς πρέπει να αφαιρέσετε το άθροισμα των δύο γωνιών κατά 180 μοίρες. Ωστόσο, υπάρχουν και άλλοι τρόποι που μπορείτε να χρησιμοποιήσετε για να βρείτε την τρίτη γωνία ενός τριγώνου εάν το σχήμα του προβλήματος είναι λίγο διαφορετικό από το συνηθισμένο. Αν θέλετε να μάθετε πώς να βρείτε την τρίτη γωνία ενός τριγώνου, ακολουθήστε τον παρακάτω οδηγό.
Βήμα
Μέθοδος 1 από 3: Χρήση των μέτρων των άλλων δύο γωνιών
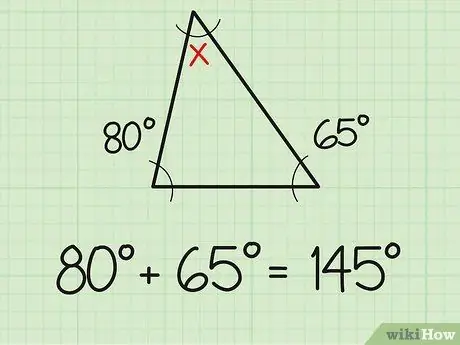
Βήμα 1. Προσθέστε τις δύο γνωστές γωνίες
Ένα γεγονός που πρέπει να γνωρίζετε είναι ότι το άθροισμα των τριών γωνιών ενός τριγώνου είναι πάντα 180 μοίρες. Έτσι, αν γνωρίζετε ήδη το μέτρο των δύο γωνιών ενός τριγώνου, η εύρεση της τρίτης γωνίας θα είναι τόσο απλή όσο το να κάνετε απλά προβλήματα πρόσθεσης και αφαίρεσης. Αρχικά, αθροίστε τα δύο μέτρα γωνίας που γνωρίζετε ήδη. Για παράδειγμα, δύο γνωστές γωνίες μετρούν 80 και 65 μοίρες. Προσθέστε τα δύο μαζί (80+65) και παίρνετε 145 μοίρες.
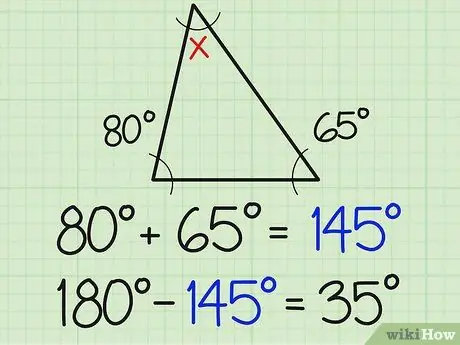
Βήμα 2. Διαιρέστε αυτόν τον αριθμό με 180
Το άθροισμα των τριών γωνιών ενός τριγώνου είναι πάντα 180 μοίρες. Επομένως, η τρίτη γωνία πρέπει να είναι 180 όταν προστίθεται στο άθροισμα των δύο γνωστών μέτρων της γωνίας. Στο παραπάνω παράδειγμα, αυτό σημαίνει 180-154 = 35.
Βήμα 3. Γράψτε την απάντησή σας
Τώρα έχετε την απάντηση στην τρίτη γωνία (στο παράδειγμα 35 μοίρες). Εάν εξακολουθείτε να αμφιβάλλετε, δείτε μόνοι σας. Προσθέστε τις τρεις γωνίες μαζί και θα έχετε ένα αποτέλεσμα 180. Αν όχι, ο υπολογισμός σας είναι λάθος. Για αυτό το παράδειγμα, 80+65+35 = 180. Εάν είναι σωστό, σημαίνει ότι έχετε λύσει το πρόβλημα.
Μέθοδος 2 από 3: Χρήση μεταβλητών
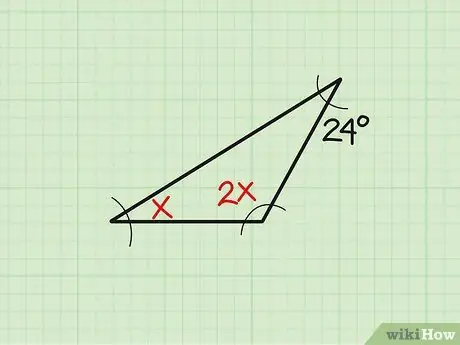
Βήμα 1. Γράψτε το πρόβλημα
Μερικές φορές, το μέγεθος της υπάρχουσας γωνίας εμφανίζεται σε μεταβλητή μορφή. Ας πάρουμε αυτό το παράδειγμα: "Βρείτε τη γωνία" x "ενός τριγώνου εάν οι τρεις γωνίες μετρούν" x "," 2x "και 24, αντίστοιχα." Αρχικά, γράψτε το πρόβλημα.
Βήμα 2. Προσθέστε όλα τα μέτρα γωνίας
Η αρχή που πρέπει να θυμάστε παραμένει η ίδια. Έτσι, πρώτα προσθέστε τις τρεις γωνίες στο πρόβλημα, δηλαδή "x+2x+24 = 3x+24".
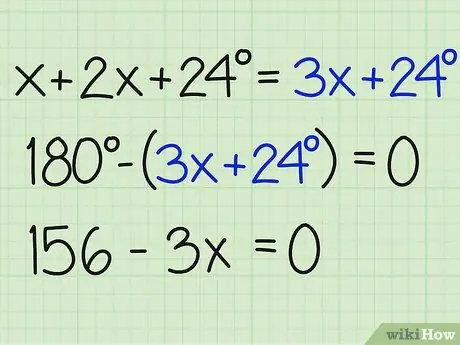
Βήμα 3. Διαιρέστε το άθροισμα των γωνιών με 180
Τώρα, διαφορά αυτού του αριθμού κατά 180 μοίρες για να βρείτε το x και να βρείτε την απάντηση στο πρόβλημα. Βεβαιωθείτε ότι τερματίζετε την εξίσωση ίση με μηδέν. Να πώς γράφεται:
- 180- (3x+24) = 0
- 180-3x-24 = 0
- 156-3x = 0
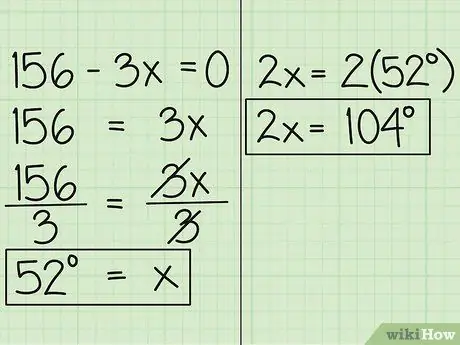
Βήμα 4. Βρείτε την τιμή του x
Τώρα, μετακινήστε τη μεταβλητή στην άλλη πλευρά της εξίσωσης και θα πάρετε 156 = 3x. Στη συνέχεια, διαιρέστε την εξίσωση με 3, οπότε παίρνετε x = 52. Αυτό σημαίνει ότι το μέτρο της γωνίας που εκφράζεται σε x είναι 52 μοίρες. Η άλλη γωνία, εκφρασμένη σε 2x είναι 52 μοίρες επί 2, που είναι 104 μοίρες.
Βήμα 5. Ελέγξτε τα αποτελέσματά σας
Αν θέλετε να βεβαιωθείτε ότι η απάντησή σας είναι σωστή, απλώς προσθέστε τα τρία μέτρα γωνίας στα οποία έχετε ήδη βρει την απάντηση. Εάν το αποτέλεσμα είναι 180, σημαίνει ότι η απάντησή σας είναι σωστή. Για αυτό το παράδειγμα, 52+104+24 = 180.
Μέθοδος 3 από 3: Χρήση άλλων μεθόδων
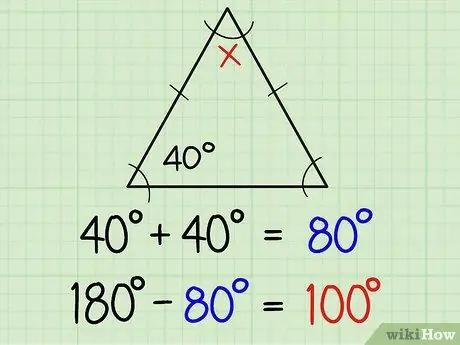
Βήμα 1. Βρείτε τις γωνίες ενός ισοσκελούς τριγώνου
Ένα ισοσκελές τρίγωνο έχει δύο ίσες πλευρές και δύο ίσες γωνίες. Δύο ίσες πλευρές επισημαίνονται συνήθως με μια μικρή γραμμή στη μέση της πλευρικής γραμμής, πράγμα που σημαίνει ότι οι δύο αντίθετες γωνίες στη γραμμή είναι το ίδιο μέτρο. Εάν γνωρίζετε ήδη το μέγεθος μιας γωνίας, γνωρίζετε αυτόματα την άλλη γωνία. Ακολουθεί περαιτέρω εξήγηση:
Εάν μία από τις ίσες γωνίες είναι 40 μοίρες, τότε η άλλη είναι 40 μοίρες. Με αυτόν τον τρόπο μπορείτε να βρείτε και τις τρεις γωνίες με τη διαφορά μεταξύ του αθροίσματος 40+40 (δηλαδή 80) και 180, ή με άλλα λόγια 180-80 = 100
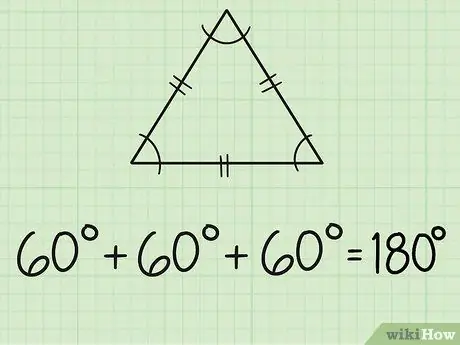
Βήμα 2. Βρείτε τις γωνίες ενός ισόπλευρου τριγώνου
Ένα ισόπλευρο τρίγωνο έχει τρεις ίσες πλευρές και τρεις ίσες γωνίες. Κάθε πλευρά συνήθως σημειώνεται με δύο σύντομες γραμμές στη μέση. Δεδομένου ότι και οι τρεις γωνίες είναι ίσες, σημαίνει ότι όλες οι γωνίες μετρούν 60 μοίρες, επειδή 180/3 = 60.
Βήμα 3. Βρείτε την τρίτη γωνία σε ορθογώνιο τρίγωνο
Ας υποθέσουμε ότι έχετε ένα ορθογώνιο τρίγωνο, με μία από τις οξείες γωνίες να έχει μέγεθος 30 μοίρες. Δεδομένου ότι το τρίγωνο είναι ορθή γωνία, σημαίνει ότι μία από τις γωνίες, δηλαδή η ορθή γωνία, πρέπει να έχει 90 μοίρες. Στη συνέχεια, χρησιμοποιήστε την αρχή του τριγώνου, τη διαφορά μεταξύ του αθροίσματος των δύο γωνιών (90+30 = 120) κατά 180, τότε θα πάρετε 180-120 = 60 μοίρες.
