- Συγγραφέας Jason Gerald gerald@how-what-advice.com.
- Public 2024-01-15 08:12.
- Τελευταία τροποποίηση 2025-01-23 12:15.
Ο διαχωρισμός με δεκαδικούς αριθμούς φαίνεται δύσκολο στην αρχή επειδή κανείς δεν σας έχει διδάξει τον πίνακα "0, 7 φορές". Το μυστικό για να γίνει αυτό είναι να μετατρέψετε το πρόβλημα διαίρεσης σε μορφή που χρησιμοποιεί μόνο ακέραιους αριθμούς. Αφού ξαναγράψετε το πρόβλημα με αυτόν τον τρόπο, θα γίνει ένα κανονικό πρόβλημα μακράς διαίρεσης.
Βήμα
Μέρος 1 από 2: Προβλήματα γραφής ως συνηθισμένα προβλήματα διαίρεσης
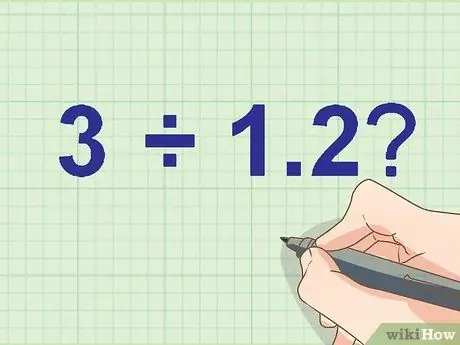
Βήμα 1. Καταγράψτε το πρόβλημα διαίρεσης
Χρησιμοποιήστε ένα μολύβι αν θέλετε να βελτιώσετε τη δουλειά σας.
-
Παράδειγμα:
Πόσα 3 ÷ 1, 2?

Βήμα 2. Γράψτε ολόκληρο τον αριθμό ως δεκαδικό
Γράψτε ένα δεκαδικό σημείο μετά τον ακέραιο αριθμό και μετά γράψτε ένα μηδέν μετά το δεκαδικό. Κάντε αυτό μέχρι και οι δύο αριθμοί να έχουν την ίδια τιμή θέσης στα δεξιά της υποδιαστολής. Αυτό δεν αλλάζει την ακέραιη τιμή.
-
Παράδειγμα:
Στο πρόβλημα 3 1, 2, ο ακέραιος αριθμός μας είναι 3. Δεδομένου ότι το 1, 2 έχει μια τιμή θέσης στα δεξιά της υποδιαστολής, γράψτε το 3 ως 3, 0, έτσι ώστε αυτός ο αριθμός να έχει επίσης μια τιμή θέσης μετά το δεκαδικό. Τώρα, το θέμα μας γίνεται 3, 0 ÷ 1, 2.
- Προειδοποίηση: μην προσθέσετε μηδενικά στα αριστερά της υποδιαστολής! Ο αριθμός 3 είναι ίσος με 3, 0 ή 3, 00, αλλά όχι ίσος με 30 ή 300.

Βήμα 3. Μετακινήστε το δεκαδικό σημείο προς τα δεξιά μέχρι να λάβετε έναν ακέραιο αριθμό
Σε προβλήματα διαίρεσης, μπορείτε να μετακινήσετε τα δεκαδικά ψηφία, αλλά μόνο εάν μετακινήσετε τα δεκαδικά ψηφία σε όλους τους αριθμούς κατά τον ίδιο αριθμό βημάτων. Αυτό σας επιτρέπει να μετατρέψετε το πρόβλημα σε ακέραιο αριθμό.
-
Παράδειγμα:
Για να μετατρέψετε 3, 0 1, 2 σε ακέραιο αριθμό, μετακινήστε το δεκαδικό ψηφίο ένα βήμα προς τα δεξιά. Έτσι, 3, 0 γίνονται 30 και 1, 2 γίνονται 12. Τώρα, το πρόβλημά μας γίνεται 30 ÷ 12.

Βήμα 4. Γράψτε το πρόβλημα χρησιμοποιώντας μακρά διαίρεση
Τοποθετήστε τον διαιρετό αριθμό (συνήθως τον μεγαλύτερο αριθμό) κάτω από το σύμβολο της μακράς διαίρεσης. Γράψτε τον διαιρέτη έξω από αυτό το σύμβολο. Τώρα, έχετε ένα κανονικό πρόβλημα μακράς διαίρεσης που χρησιμοποιεί ακέραιους αριθμούς. Αν θέλετε μια υπενθύμιση για το πώς να κάνετε μακροχρόνια διαίρεση, διαβάστε την επόμενη ενότητα.
Μέρος 2 από 2: Επίλυση προβλημάτων μακράς διαίρεσης

Βήμα 1. Βρείτε το πρώτο ψηφίο της απάντησης
Ξεκινήστε να λύνετε αυτό το πρόβλημα όπως θα κάνατε συνήθως, συγκρίνοντας τον διαιρέτη και το πρώτο ψηφίο του διαιρεμένου αριθμού. Υπολογίστε το αποτέλεσμα της διαίρεσης αυτού του πρώτου ψηφίου με τον αριθμό του διαιρέτη και, στη συνέχεια, γράψτε το αποτέλεσμα πάνω από αυτό το ψηφίο.
Παράδειγμα: Προσπαθούμε να διαιρέσουμε το 30 με το 12. Συγκρίνετε το 12 με το πρώτο ψηφίο του αριθμού που διαιρείται, το οποίο είναι 3. Δεδομένου ότι το 12 είναι μεγαλύτερο από το 3, το 3 διαιρείται με το 12 ίσο με 0. Γράψτε 0 πάνω από 3 στη γραμμή απαντήσεων.
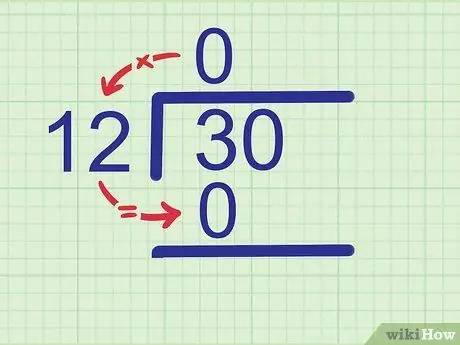
Βήμα 2. Πολλαπλασιάστε το πηλίκο με τον διαιρέτη
Γράψτε το γινόμενο του προϊόντος με τον αριθμό που διαιρείται. Γράψτε το αποτέλεσμα ακριβώς κάτω από το πρώτο ψηφίο του αριθμού που διαιρέσατε γιατί αυτό είναι το ψηφίο που μόλις είδατε.
-
Παράδειγμα:
Αφού 0 x 12 = 0, γράψτε 0 κάτω από 3
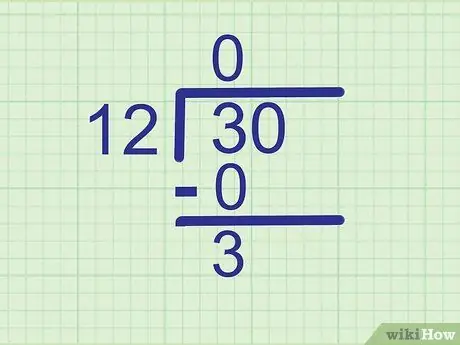
Βήμα 3. Αφαιρέστε για να βρείτε το υπόλοιπο
Αφαιρέστε το προϊόν που μόλις υπολογίσατε από το ψηφίο ακριβώς πάνω του. Γράψτε την απάντηση σε μια νέα γραμμή, κάτω από αυτήν.
-
Παράδειγμα:
3 - 0 = 3, οπότε γράψτε
Βήμα 3. λίγο κάτω από το 0.
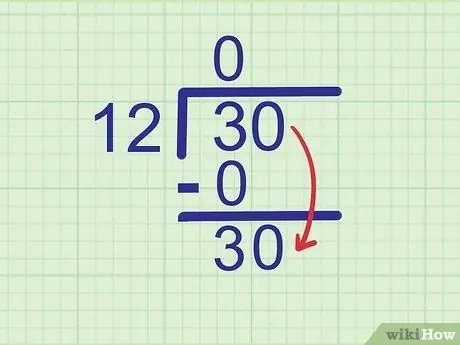
Βήμα 4. Χαμηλώστε το επόμενο ψηφίο
Αφήστε το επόμενο ψηφίο του διαιρεμένου αριθμού δίπλα στον αριθμό που μόλις γράψατε.
-
Παράδειγμα:
Ο αριθμός που διαιρείται είναι 30. Είδαμε τον αριθμό 3, οπότε το επόμενο ψηφίο που πρέπει να χαμηλώσει είναι 0. Μειώστε τον αριθμό 0 στην πλευρά του 3 ώστε να γίνει
Βήμα 30..
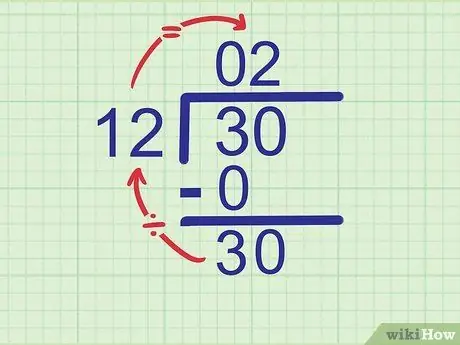
Βήμα 5. Δοκιμάστε να διαιρέσετε τον νέο αριθμό με τον διαιρέτη
Τώρα, επαναλάβετε το πρώτο βήμα σε αυτήν την ενότητα για να βρείτε το δεύτερο ψηφίο της απάντησής σας. Αυτή τη φορά, συγκρίνετε τον διαιρέτη με τον αριθμό που μόλις γράψατε στην κάτω σειρά.
-
Παράδειγμα:
Ποιο είναι το πηλίκο του 30 επί 12; Η πλησιέστερη απάντηση που μπορούμε να πάρουμε είναι 2 γιατί 12 x 2 = 24. Γράψτε
Βήμα 2. στη δεύτερη θέση στη γραμμή απαντήσεων.
- Εάν δεν είστε σίγουροι για την απάντηση, δοκιμάστε πολλαπλασιασμούς μέχρι να βρείτε τη μεγαλύτερη απάντηση που ταιριάζει. Για παράδειγμα, εάν η εκτίμησή σας είναι 3, υπολογίστε 12 x 3 και παίρνετε 36. Αυτός ο αριθμός είναι πολύ μεγάλος επειδή προσπαθούμε να υπολογίσουμε 30. Δοκιμάστε να χαμηλώσετε έναν αριθμό, 12 x 2 = 24. Αυτός ο αριθμός ταιριάζει. Έτσι, το 2 είναι η σωστή απάντηση.

Βήμα 6. Επαναλάβετε τα παραπάνω βήματα για να βρείτε τον επόμενο αριθμό
Αυτή είναι η ίδια διαδικασία μακράς διαίρεσης όπως χρησιμοποιήθηκε παραπάνω και για οποιοδήποτε πρόβλημα μακράς διαίρεσης:
- Πολλαπλασιάστε το νέο ψηφίο της απάντησής σας με τον διαιρέτη: 2 x 12 = 24.
- Γράψτε το προϊόν σε μια νέα γραμμή, κάτω από τον αριθμό που διαιρέθηκε: Γράψτε 24 ακριβώς κάτω από το 30.
- Αφαιρέστε την κάτω σειρά από τη σειρά πάνω από αυτήν: 30 - 24 = 6. Έτσι, γράψτε 6 σε μια νέα σειρά από κάτω.

Βήμα 7. Συνεχίστε αυτήν τη διαδικασία μέχρι να ολοκληρώσετε την τελευταία σειρά απαντήσεων
Εάν εξακολουθούν να υπάρχουν ψηφία στον διαιρεμένο αριθμό, χαμηλώστε τα ψηφία προς τα κάτω και συνεχίστε την επίλυση του προβλήματος με τον ίδιο τρόπο. Εάν έχετε ολοκληρώσει την τελευταία σειρά απαντήσεων, συνεχίστε στο επόμενο βήμα.
-
Παράδειγμα:
Μόλις γράψαμε
Βήμα 2. στην τελευταία γραμμή απαντήσεων. Προχωρήστε στο επόμενο βήμα.

Βήμα 8. Προσθέστε δεκαδικά ψηφία για να "επεκτείνετε" τον διαιρεμένο αριθμό, εάν χρειάζεται
Εάν ο αριθμός είναι ομοιόμορφα διαιρέσιμος, το τελικό αποτέλεσμα αφαίρεσης είναι "0". Αυτό σημαίνει ότι έχετε ολοκληρώσει τη διαίρεση και λαμβάνετε μια απάντηση με τη μορφή ενός ακέραιου αριθμού. Ωστόσο, εάν έχετε ολοκληρώσει την τελευταία γραμμή απαντήσεων και υπάρχουν ακόμη ψηφία που μπορούν να διαιρεθούν, θα πρέπει να "επεκτείνετε" τον διαιρούμενο αριθμό προσθέτοντας ένα δεκαδικό σημείο ακολουθούμενο από τον αριθμό 0. Λάβετε υπόψη ότι αυτό δεν Δεν αλλάζω την τιμή του αριθμού.
-
Παράδειγμα:
Φτάσαμε στην τελευταία σειρά απαντήσεων, αλλά η απάντηση στην τελευταία αφαίρεση μας είναι "6". Γράψτε "6, 0" κάτω από το σύμβολο μακράς διαίρεσης προσθέτοντας ", 0" στο τελευταίο ψηφίο. Γράψτε επίσης το δεκαδικό σημείο στο ίδιο σημείο στη γραμμή απαντήσεων, αλλά μην γράψετε τίποτα μετά από αυτό.

Βήμα 9. Επαναλάβετε τα ίδια βήματα για να βρείτε το επόμενο ψηφίο
Η μόνη διαφορά εδώ είναι ότι πρέπει να προσθέσετε το δεκαδικό σημείο στο ίδιο σημείο στη γραμμή απαντήσεων. Μόλις το κάνετε αυτό, μπορείτε να αναζητήσετε τα υπόλοιπα ψηφία απάντησης με τον ίδιο ακριβώς τρόπο.
-
Παράδειγμα:
Ρίξτε το νέο 0 κάτω στην τελευταία γραμμή, έτσι ώστε να γίνει "60". Δεδομένου ότι το 60 διαιρούμενο με το 12 είναι ακριβώς 5, γράψτε
Βήμα 5. ως το τελευταίο ψηφίο της γραμμής απαντήσεών μας. Μην ξεχνάτε ότι βάζουμε ένα δεκαδικό στη γραμμή απάντησης. Ετσι, 2, 5 είναι η τελική απάντηση στην ερώτησή μας.
Συμβουλές
- Μπορείτε να το γράψετε ως υπόλοιπο (οπότε η απάντηση στα 3 1, 2 είναι "2 υπόλοιπα 6"). Ωστόσο, επειδή εργάζεστε με δεκαδικά ψηφία, ο δάσκαλός σας μπορεί να περιμένει από εσάς να εργαστείτε στο δεκαδικό τμήμα της απάντησης.
- Εάν ακολουθείτε σωστά τη μέθοδο της μακράς διαίρεσης, θα έχετε πάντα ένα δεκαδικό σημείο στη σωστή θέση ή καθόλου δεκαδικό σημείο εάν ο αριθμός διαιρείται με διαιρέσιμο. Μην προσπαθήσετε να μαντέψετε τα δεκαδικά ψηφία. Το δεκαδικό ψηφίο είναι συχνά διαφορετικό από το δεκαδικό στον αρχικό αριθμό.
- Εάν το πρόβλημα της μακράς διαίρεσης δεν διαρκέσει για μεγάλο χρονικό διάστημα, μπορείτε να σταματήσετε και να στρογγυλέψετε στον πλησιέστερο αριθμό. Για παράδειγμα, για να λύσετε 17 4, 2, απλά μετρήστε έως το 4.047… και στρογγυλοποιήστε την απάντησή σας στο "περίπου 4.05".
-
Θυμηθείτε τους όρους διαίρεσης:
- Ο αριθμός που πρέπει να διαιρεθεί είναι ο αριθμός που πρέπει να διαιρεθεί.
- Ο διαιρέτης είναι ο αριθμός που χρησιμοποιείται για τη διαίρεση.
- Το πηλίκο είναι η απάντηση στο πρόβλημα της μαθηματικής διαίρεσης.
- Ολόκληρο: Διαιρούμενο με διαιρέτη = πηλίκο.
Προειδοποίηση
Θυμηθείτε ότι το 30 12 θα δώσει την ίδια απάντηση με το 3 1, 2. Μην προσπαθήσετε να "διορθώσετε" την απάντησή σας αφού μετακινήσετε το δεκαδικό προς τα πίσω
Σχετικά άρθρα wikiHow
- Μετατροπή κοινών κλασμάτων σε δεκαδικά ψηφία
- Κάνοντας Μεγάλο Αποφασισμένο Τμήμα
- Διαίρεση κλασμάτων ανά κλάσματα
- Διαίρεση μικτών κλασμάτων






