Ο πολλαπλασιασμός είναι ένας τρόπος επίλυσης εξισώσεων που περιλαμβάνουν μεταβλητή δύο ισοδύναμων κλασμάτων. Μια μεταβλητή είναι ένα σύμβολο κράτησης θέσης για μια άγνωστη ποσότητα αριθμών και ο πολλαπλασιασμός την μετατρέπει σε μια απλή εξίσωση, επιτρέποντάς σας να βρείτε την τιμή της εν λόγω μεταβλητής. Ο πολλαπλασιασμός είναι πολύ χρήσιμος όταν θέλετε να ολοκληρώσετε μια σύγκριση. Δείτε πώς να το κάνετε:
Βήμα
Μέθοδος 1 από 2: Διασταυρούμενο προϊόν μιας μεταβλητής
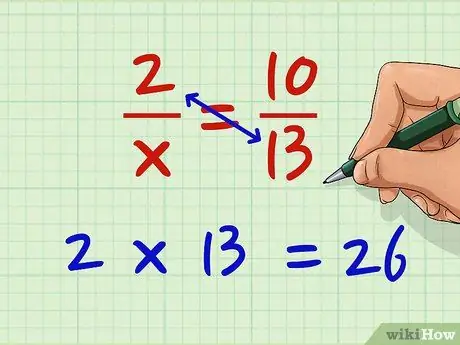
Βήμα 1. Πολλαπλασιάστε τον αριθμητή του αριστερού κλάσματος με τον παρονομαστή του δεξιού κλάσματος
Πείτε ότι θέλετε να λύσετε την εξίσωση 2/x = 10/13. Τώρα, πολλαπλασιάστε το 2 επί 13,2 x 13 = 26.
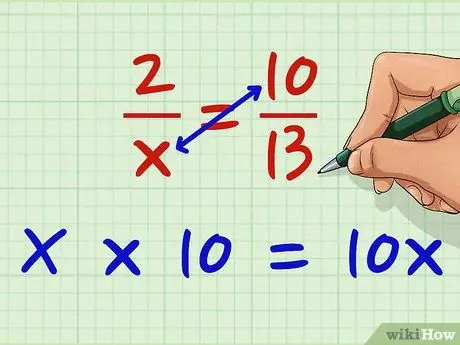
Βήμα 2. Πολλαπλασιάστε τον παρονομαστή του δεξιού χεριού με τον παρονομαστή του αριστερού
Πολλαπλασιάστε x με 10. X * 10 = 10x. Μπορείτε πρώτα να διασχίσετε αυτήν την ενότητα. δεν έχει σημασία αρκεί να πολλαπλασιάσετε και τους δύο αριθμητές με τους δύο παρονομαστές διαγώνια.
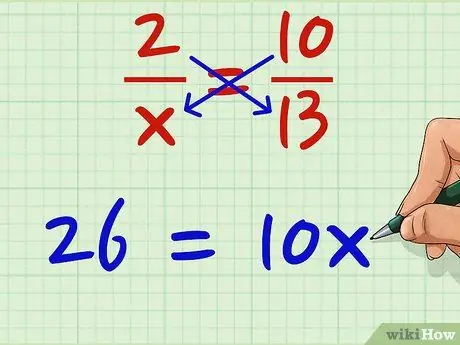
Βήμα 3. Κάντε τα δύο προϊόντα ίσα
26 ισοδυναμεί με 10x. 26 = 10x Δεν έχει σημασία ποια είναι δεξιά ή αριστερά. όντας ίσοι, μπορείτε να αλλάξετε την τοποθεσία τους αρκεί να τα μετακινήσετε όλα ταυτόχρονα.
Αν προσπαθήσετε λοιπόν να βρείτε την τιμή x 2/x = 10/13, 2 * 13 = x * 10 ή 26 = 10x
Βήμα 4. Βρείτε την τιμή της μεταβλητής
Τώρα που έχετε 26 = 10x, μπορείτε να προσπαθήσετε να βρείτε έναν κοινό αριθμητή και να διαιρέσετε τα 26 και 10 με τον ίδιο αριθμό που διαιρεί και τα δύο. Δεδομένου ότι και οι δύο είναι άρτιοι αριθμοί, μπορείτε να διαιρέσετε με 2. 26/2 = 13 και 10/2 = 5. Το υπόλοιπο είναι 13 = 5x. Τώρα, παίρνοντας το x μόνο, διαιρέστε και τις δύο πλευρές της εξίσωσης με το 5. Άρα 13/5 = 5/5 ή 13/5 = x. Εάν θέλετε την απάντηση σε δεκαδική μορφή, μπορείτε να ξεκινήσετε διαιρώντας και τις δύο πλευρές της εξίσωσης με το 10 για να πάρετε 26/10 = 10/10 ή 2,6 = x.
Μέθοδος 2 από 2: Πολυμεταβλητός Σταυρός Πολλαπλασιασμός
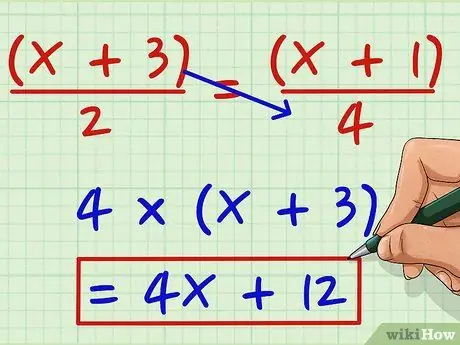
Βήμα 1. Πολλαπλασιάστε τον αριθμητή στα αριστερά με τον παρονομαστή στα δεξιά
Πείτε ότι θέλετε να λύσετε την ακόλουθη εξίσωση: (x + 3)/2 = (x + 1)/4. Πολλαπλασιάστε (x + 3) επί 4 για να πάρετε 4 (x + 3). Πολλαπλασιάστε με 4 για να πάρετε 4x + 12.
Βήμα 2. Πολλαπλασιάστε τον αριθμητή στα δεξιά με τον παρονομαστή στα αριστερά
Επαναλάβετε τη διαδικασία από την άλλη πλευρά. (x+1) x 2 = 2 (x+1). Πολλαπλασιάστε με 2 για να πάρετε 2x + 2.
Βήμα 3. Κάντε το γινόμενο των δύο ίσων και συνδυάστε τις ίδιες μεταβλητές
Τώρα, το αποτέλεσμα είναι 4x + 12 = 2x + 2. Συνδυάστε τη μεταβλητή x και τη σταθερά στην άλλη πλευρά της εξίσωσης.
- Έτσι, συνδυάστε 4x και 2x αφαιρώντας 2x και από τις δύο πλευρές. Η αφαίρεση 2x από 2x θα αφήσει ένα υπόλοιπο 0. Στα αριστερά, 4x - 2x = 2x, οπότε το υπόλοιπο είναι 2x.
- Τώρα, συνδυάστε 12 και 2 αφαιρώντας το 12 και από τις δύο πλευρές. Αφαιρέστε το 12 από το 12 στην αριστερή πλευρά και το αποτέλεσμα είναι 0, στη συνέχεια αφαιρέστε το 12 από το 2 στη δεξιά πλευρά, έτσι ώστε το αποτέλεσμα να είναι 2 -12 = -10.
- Το υπόλοιπο είναι 2x = -10.
Βήμα 4. Τελειώστε
Το μόνο που έχετε να κάνετε είναι να διαιρέσετε και τις δύο πλευρές της εξίσωσης με 2. 2x/2 = -10/2 = x = -5. Μετά τον πολλαπλασιασμό σταυρών, διαπιστώνετε ότι x = -5. Μπορείτε να επιστρέψετε και να ελέγξετε την εργασία σας εισάγοντας την τιμή x, η οποία είναι -5 για να βεβαιωθείτε ότι και οι δύο πλευρές είναι ίσες. Αποδείχθηκε ισοδύναμο. Εάν συνδέσετε το -5 στην αρχική εξίσωση, το αποτέλεσμα είναι -1 = -1.
Συμβουλές
- Σημειώστε ότι εάν συνδέσετε διαφορετικούς αριθμούς (ας πούμε 5) στην ίδια εξίσωση, το αποτέλεσμα είναι 2/5 = 10/13. Ακόμα κι αν πολλαπλασιάσετε την αριστερή πλευρά με άλλα 5/5, παίρνετε 10/25 = 10/13, κάτι που είναι σαφώς λάθος. Αυτή η περίπτωση υποδεικνύει ότι κάνατε σφάλμα πολλαπλασιασμού.
- Μπορείτε να ελέγξετε την απάντησή σας συνδέοντας το αποτέλεσμα στην αρχική εξίσωση. Εάν η εξίσωση είναι μια αληθινή πρόταση, για παράδειγμα 1 = 1, η απάντησή σας είναι σωστή. Εάν η εξίσωση γίνει ψευδής δήλωση, για παράδειγμα 0 = 1, κάνατε λάθος. Για παράδειγμα, συνδέστε 2, 6 στην εξίσωση έτσι ώστε 2/(2, 6) = 10/13. Πολλαπλασιάστε την αριστερή πλευρά με 5/5 για να πάρετε 10/13 = 10/13. Το αποτέλεσμα είναι μια σωστή πρόταση, η οποία όταν απλοποιηθεί γίνεται 1 = 1, άρα 2, 6 είναι η σωστή απάντηση.
